Curvature line
From Encyclopedia of Mathematics
A line on a surface at each point of which the tangent has one of the principal directions. The curvature lines are defined by the equation
 |
where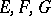 
are the coefficients of the first fundamental form of the surface, and 
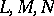those of the second fundamental form. The normals to the surface along curvature lines form a developable surface. The curvature lines on a surface of revolution are the meridians and the parallels of latitude. The curvature lines on a developable surface are its generators (which are straight lines) and the lines orthogonal to them.
Comments
References
| [a1] | D.J. Struik, "Differential geometry" , Addison-Wesley (1950) |
How to Cite This Entry:
Curvature line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_line&oldid=19095
Curvature line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature_line&oldid=19095
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article