Cubic equation
An algebraic equation of degree three, i.e. an equation of the form
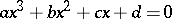 |
where 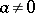 . Replacing
. Replacing  in this equation by the new unknown
in this equation by the new unknown 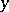 defined by
defined by 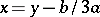 , one brings the equation to the following simpler (canonical) form:
, one brings the equation to the following simpler (canonical) form:
 |
where
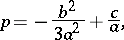 |
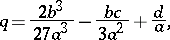 |
and the solution to this equation may be obtained by using Cardano's formula (cf. Cardano formula); in other words, any cubic equation is solvable in radicals.
The cubic equation was first solved in the 16th century. At the beginning of that century, S. Ferro solved the equation 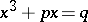 , where
, where 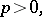 ,
, 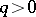 , but did not publish his solution. N. Tartaglia rediscovered Ferro's result; he also solved the equation
, but did not publish his solution. N. Tartaglia rediscovered Ferro's result; he also solved the equation 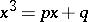 (
(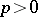 ,
, 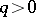 ), and announced without proof that the equation
), and announced without proof that the equation 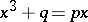 (
(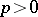 ,
, 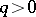 ) could be reduced to that form. Tartaglia communicated his results to G. Cardano, who published the solution of the general cubic equation in 1545.
) could be reduced to that form. Tartaglia communicated his results to G. Cardano, who published the solution of the general cubic equation in 1545.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
The history is treated in [a2], where Cardano's name (wrongly) occurs as Cardan (Chapt. 12).
References
| [a1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [a2] | W.W. Rouse Ball, "A short account of the history of mathematics" , Dover, reprint (1960) pp. 123–125 |
Cubic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cubic_equation&oldid=15586