Crossed homomorphism
of a group 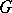 into a group
into a group 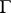 with group of operators
with group of operators 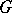
A mapping 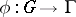 satisfying the condition
satisfying the condition 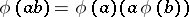 . If
. If 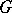 acts trivially on
acts trivially on 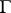 , then crossed homomorphisms are just ordinary homomorphisms. Crossed homomorphisms are also called
, then crossed homomorphisms are just ordinary homomorphisms. Crossed homomorphisms are also called 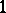 -cocycles of
-cocycles of 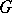 with values in
with values in 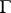 (see Non-Abelian cohomology). Every element
(see Non-Abelian cohomology). Every element 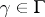 defines a crossed homomorphism
defines a crossed homomorphism 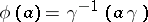 (
(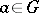 ), called a principal crossed homomorphism, or cocycle cohomologous to
), called a principal crossed homomorphism, or cocycle cohomologous to  . A mapping
. A mapping 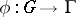 is a crossed homomorphism if and only if the mapping
is a crossed homomorphism if and only if the mapping 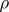 of
of 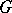 into the holomorph of
into the holomorph of 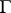 (cf. Holomorph of a group) given by
(cf. Holomorph of a group) given by 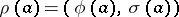 , where
, where 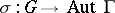 is the homomorphism defining the
is the homomorphism defining the 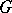 action on
action on 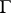 , is a homomorphism. For example, if
, is a homomorphism. For example, if 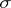 is a linear representation of
is a linear representation of 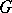 in a vector space
in a vector space 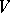 , then any crossed homomorphism
, then any crossed homomorphism 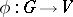 defines a representation
defines a representation 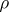 of
of 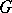 by affine transformations of
by affine transformations of 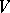 . The set
. The set 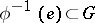 is called the kernel of the crossed homomorphism
is called the kernel of the crossed homomorphism 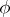 ; it is always a subgroup of
; it is always a subgroup of 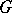 .
.
Comments
References
| [a1] | S. MacLane, "Homology" , Springer (1963) |
| [a2] | S. Lang, "Rapport sur la cohomologie des groupes" , Benjamin (1966) |
Crossed homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Crossed_homomorphism&oldid=18894