Difference between revisions of "Crossed complex"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 76 formulas, 75 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
Crossed complexes are a variant of chain complexes of modules over integral group rings but strengthened in two ways: | Crossed complexes are a variant of chain complexes of modules over integral group rings but strengthened in two ways: | ||
| − | i) in general, they are non-commutative in dimensions | + | i) in general, they are non-commutative in dimensions $1$ and $2$; and |
| − | ii) they are based on groupoids rather than groups. More specifically, the part | + | ii) they are based on groupoids rather than groups. More specifically, the part $C _ { 2 } \rightarrow C _ { 1 } \underset{\rightarrow}{\rightarrow} C _ { 0 }$ is a [[Crossed module|crossed module]] of groupoids. An advantage of i) is that allows for crossed complexes to encode information on presentations of groups, or, through ii), of groupoids. An advantage of ii) is that it allows the modeling of cell complexes with many base points. This is necessary for modeling: the geometry of simplices; covering spaces, and in particular Cayley graphs; and the equivariant theory. It is also essential for the [[Closed category|closed category]] structure on the category of crossed complexes. However, the reduced case, i.e. when $C _ { 0 }$ is a singleton, is also important. |
| − | Crossed complexes arise naturally from relative homotopy theory (cf. also [[Homotopy|Homotopy]]) as follows. A filtered space | + | Crossed complexes arise naturally from relative homotopy theory (cf. also [[Homotopy|Homotopy]]) as follows. A filtered space $X_{*}$ is a sequence $( X _ { n } ) _ { n \geq 0}$ of increasing subspaces of a space $X _ { \infty }$. One easily gets a [[Category|category]] $\mathcal{FT} \operatorname {op}$ of filtered spaces. There is a homotopy crossed complex functor $\pi : \mathcal{FT} \text{op} \rightarrow \mathcal{C} \text{rs}$, defined using the fundamental groupoid $\pi _ { 1 } ( X _ { 1 } , X _ { 0 } )$ (cf. also [[Fundamental group|Fundamental group]]), the relative homotopy groups $\pi _ { n } ( X _ { n } , X _ { n - 1} , x )$, $n \geq 2$, $x \in X _ { 0 }$ (cf. also [[Homotopy group|Homotopy group]]), and appropriate boundary mappings and actions. Using geometric realization and the skeletal filtration, one gets a functor from simplicial sets to crossed complexes (cf. also [[Simplicial set|Simplicial set]]). This has a left adjoint $N$, the nerve, and from this one gets the classifying space functor $\mathcal{B} : \mathcal{C} \text{rs} \rightarrow \mathcal{FT} \text{op}$, for which $( \mathcal{BC} ) _ { \infty }$ is called the classifying space of the crossed complex $C$ (cf. also [[Classifying space|Classifying space]]). There is a natural isomorphism $\pi ( \mathcal{B} C ) \cong C$, which shows that the axioms for a crossed complex are exactly the properties universally held by the topological example $\pi X_{*} $. |
| − | The category | + | The category $\mathcal{C} \text{rs}$ of crossed complexes is symmetric monoidal closed (cf. also [[Category|Category]]; [[Closed category|Closed category]]; [[Monoid|Monoid]]), so that for any crossed complexes $A$, $B$, $C$ there is a tensor product $A \otimes B$ and an internal Hom $\operatorname{CRS}( B , C )$ with a natural bijection $\mathcal{C}\operatorname { rs } ( A \otimes B , C ) \cong \mathcal{C}\operatorname { rs } ( A , \operatorname { CRS } ( B , C ) )$. The elements of degree $0$ and $1$ in $\operatorname{CRS}( B , C )$ are, respectively, the morphisms $B \rightarrow C$ and the homotopies of such morphisms. So one can form the set $[ B , C ]$ of homotopy classes of morphisms $B \rightarrow C$. A homotopy classification theorem is that if $X_{*}$ is the skeletal filtration of a [[CW-complex|CW-complex]] $X$, then there is a natural weak homotopy equivalence $B ( \operatorname{CRS} ( \pi ( X_{ * } ) , C ) ) \rightarrow ( B C ) ^ { X }$ which induces a natural bijection $[ \pi ( X _* ) , C ] \cong [ X , B C ]$. This includes results on the homotopy classification of mappings into Eilenberg–MacLane spaces, including the case of local coefficients (cf. also [[Eilenberg–MacLane space|Eilenberg–MacLane space]]). |
| − | There is a generalized Van Kampen theorem [[#References|[a5]]], stating that the functor | + | There is a generalized Van Kampen theorem [[#References|[a5]]], stating that the functor $\pi : \mathcal{FT} \text{op} \rightarrow \mathcal{C} \text{rs}$ preserves certain colimits. This specializes to the [[Crossed module|crossed module]] case. It also implies the relative Hurewicz theorem (an advantage of this deduction is its generalization to the $n$-adic situation [[#References|[a7]]]). |
| − | The proof of the generalized Van Kampen theorem given in [[#References|[a5]]] generalizes the methods of the usual proof of the | + | The proof of the generalized Van Kampen theorem given in [[#References|[a5]]] generalizes the methods of the usual proof of the $1$-dimensional theorem, by introducing the category $\omega$-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120280/c12028041.png"/> of cubical $\omega$-groupoids, and a functor $\rho : {\cal F T} \operatorname{op} \rightarrow \omega \square \operatorname{Gpd}$, together with an equivalence of categories $\gamma : \omega \square \operatorname{Gpd} \rightarrow \mathcal{C} \operatorname{rs}$ such that $\gamma \rho$ is naturally equivalent to $\pi$. Three properties of the algebraic objects $\omega$-groupoids that are necessary for the proof are: |
a) an expression for an algebraic inverse to subdivision; | a) an expression for an algebraic inverse to subdivision; | ||
| Line 17: | Line 25: | ||
b) an expression for the homotopy addition lemma; | b) an expression for the homotopy addition lemma; | ||
| − | c) a method for dealing with compositions of homotopy addition lemma situations. The proofs that | + | c) a method for dealing with compositions of homotopy addition lemma situations. The proofs that $\rho ( X_{ *} )$ is an $\omega$-groupoid, i.e. is a form of higher homotopy groupoid, and is equivalent to $\pi ( X_{*} )$, are non-trivial. |
| − | There are other categories equivalent to | + | There are other categories equivalent to $\mathcal{C} \text{rs}$, for example those of certain kinds of simplicial groups, and of so-called simplicial $T$-complexes, which are simplicial sets with distinguished thin elements and which are Kan complexes in a strong sense [[#References|[a1]]] (see also [[Simplicial set|Simplicial set]]). The latter equivalence uses the nerve functor $N$ and generalizes the so-called Dold–Kan relation between chain complexes and simplicial Abelian groups. There is also an equivalence with a category of globular $\infty$-groupoids [[#References|[a6]]], and this shows a relation with multiple category theory [[#References|[a12]]], p. 574. Also, the [[Tensor product|tensor product]] of crossed complexes corresponds to a tensor product of $\infty$-groupoids which extends for the groupoid case a tensor product of $2$-categories due to A. Gray [[#References|[a12]]], § 6. |
| − | There is a functor from | + | There is a functor from $\mathcal{C} \text{rs}$ to a category of chain complexes of modules of groupoids, and which has a right adjoint. This enables a link with classical concepts of the [[Cohomology of groups|cohomology of groups]]. It also relates crossed complexes to the Fox free differential calculus defined for a presentation of a group. However, crossed complexes do carry more information than the corresponding chain complex. In particular, one can define free crossed complexes; the special case of free crossed resolutions is convenient for determining a presentation for the module of identities among relations for a presentation of a group. |
| − | The general background to the use of reduced crossed complexes and their analogues in other algebraic settings, and as a tool in non-Abelian homological algebra, is given in [[#References|[a10]]]. This paper also shows that the use of crossed complexes to give representatives of cohomology groups | + | The general background to the use of reduced crossed complexes and their analogues in other algebraic settings, and as a tool in non-Abelian homological algebra, is given in [[#References|[a10]]]. This paper also shows that the use of crossed complexes to give representatives of cohomology groups $H ^ { n + 1 } ( G , A )$ of a group $G$ with coefficients in a $G$-module $A$ is a special case of results on a cohomology theory for algebras relative to a variety. |
| − | The Eilenberg–Zil'ber theorem (see [[Simplicial set|Simplicial set]]) for the chain complex of a product | + | The Eilenberg–Zil'ber theorem (see [[Simplicial set|Simplicial set]]) for the chain complex of a product $K \times L$ of simplicial sets $K$, $L$ has been generalized to a natural strong deformation retraction from $\pi ( K \times L ) \rightarrow \pi ( K ) \otimes \pi ( L )$ (cf. also [[Deformation retract|Deformation retract]]). This allows for small models of homotopy colimits of crossed complexes. |
Crossed complexes do form a closed model homotopy category in the sense of D. Quillen, but stronger results in some areas, such as equivariant theory [[#References|[a4]]], can be obtained by constructing the appropriate [[Homotopy coherence|homotopy coherence]] theory and the above homotopy colimits. | Crossed complexes do form a closed model homotopy category in the sense of D. Quillen, but stronger results in some areas, such as equivariant theory [[#References|[a4]]], can be obtained by constructing the appropriate [[Homotopy coherence|homotopy coherence]] theory and the above homotopy colimits. | ||
| Line 31: | Line 39: | ||
References to many of the above facts are given in [[#References|[a3]]], [[#References|[a15]]]. | References to many of the above facts are given in [[#References|[a3]]], [[#References|[a15]]]. | ||
| − | In Baues' scheme of algebraic [[Homotopy|homotopy]] [[#References|[a2]]], reduced crossed complexes are called crossed chain complexes and are regarded as the linear models of pointed homotopy types. Extra quadratic information can be carried by crossed complexes | + | In Baues' scheme of algebraic [[Homotopy|homotopy]] [[#References|[a2]]], reduced crossed complexes are called crossed chain complexes and are regarded as the linear models of pointed homotopy types. Extra quadratic information can be carried by crossed complexes $A$ with an algebra structure $A \otimes A \rightarrow A$ satisfying the usual monoid conditions. These form a non-Abelian generalization of DG-algebras. They are also a context for some notions of higher-order symmetry and for algebraic models of $3$-types. |
| − | Another generalization of crossed modules is that of crossed | + | Another generalization of crossed modules is that of crossed $n$-cubes of groups. These are remarkable for modeling all pointed, connected homotopy $n$-types. They are equivalent to certain kinds of $n$-fold groupoids [[#References|[a8]]]. Thus, in answer to questions in the early part of the 20th century, there are higher-dimensional generalizations of the [[Fundamental group|fundamental group]], retaining its non-commutative nature, but which take the form of higher homotopy groupoids rather than higher homotopy groups. |
Although crossed complexes form only a limited model of homotopy types, their nice formal properties as described above make them a useful tool for extending chain complex methods in a geometric and more powerful manner. This was part of the motivation for applications by J.H.C. Whitehead in combinatorial homotopy theory and simple homotopy theory [[#References|[a13]]], [[#References|[a14]]], which are generalized in [[#References|[a2]]]. Whitehead's term homotopy systems for reduced free crossed complexes is also used in [[#References|[a11]]], where applications are given to [[Morse theory|Morse theory]]. | Although crossed complexes form only a limited model of homotopy types, their nice formal properties as described above make them a useful tool for extending chain complex methods in a geometric and more powerful manner. This was part of the motivation for applications by J.H.C. Whitehead in combinatorial homotopy theory and simple homotopy theory [[#References|[a13]]], [[#References|[a14]]], which are generalized in [[#References|[a2]]]. Whitehead's term homotopy systems for reduced free crossed complexes is also used in [[#References|[a11]]], where applications are given to [[Morse theory|Morse theory]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> N.D. Ashley, "Simplicial T-complexes: a non-abelian version of a theorem of Dold–Kan" ''Dissert. Math.'' , '''165''' (1988) (PhD Thesis Univ. Wales, 1976)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> H.-J. Baues, "Algebraic homotopy" , Cambridge Univ. Press (1989)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> R. Brown, "Computing homotopy types using crossed $n$-cubes of groups" N. Ray (ed.) G. Walker (ed.) , ''Adams Memorial Symposium on Algebraic Topology'' , '''1''' , Cambridge Univ. Press (1992) pp. 187–210</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R. Brown, M. Golasinski, T. Porter, A. Tonks, "On function spaces of equivariant maps and the equivariant homotopy theory of crossed complexes" ''Indag. Math.'' , '''8''' (1997) pp. 157–172</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R. Brown, P.J. Higgins, "Colimit theorems for relative homotopy groups" ''J. Pure Appl. Algebra'' , '''22''' (1981) pp. 11–41</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Brown, P.J. Higgins, "The equivalence of $\infty$-groupoids and crossed complexes" ''Cah. Topol. Géom. Diff.'' , '''22''' (1981) pp. 371–386</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> R. Brown, J.-L. Loday, "Homotopical excision, and Hurewicz theorems, for $n$-cubes of spaces" ''Proc. London Math. Soc.'' , '''54''' (1987) pp. 176–192</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> G.J. Ellis, R. Steiner, "Higher-dimensional crossed modules and the homotopy groups of $( n + 1 )$-ads" ''J. Pure Appl. Algebra'' , '''46''' (1987) pp. 117–136</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> J. Huebschmann, "Crossed $N$-fold extensions and cohomology" ''Comment. Math. Helvetici'' , '''55''' (1980) pp. 302–314</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> A.S.-T. Lue, "Cohomology of groups relative to a variety" ''J. Algebra'' , '''69''' (1981) pp. 155–174</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> V.V. Sharko, "Functions on manifolds: Algebraic and topological aspects" , ''Transl. Math. Monogr.'' , '''113''' , Amer. Math. Soc. (1993)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> R. Street, "Categorical structures" M. Hazewinkel (ed.) , ''Handbook of Algebra'' , '''I''' , Elsevier (1996) pp. 531–577</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> J.H.C. Whitehead, "Combinatorial homotopy II" ''Bull. Amer. Math. Soc.'' , '''55''' (1949) pp. 453–496</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> J.H.C. Whitehead, "Simple homotopy types" ''Amer. J. Math.'' , '''72''' (1950) pp. 1–57</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> R. Brown, "Groupoids and crossed objects in algebraic topology" ''Homology, Homotopy and Appl.'' , '''1''' (1999) pp. 1–78</td></tr></table> |
Revision as of 17:44, 1 July 2020
Crossed complexes are a variant of chain complexes of modules over integral group rings but strengthened in two ways:
i) in general, they are non-commutative in dimensions $1$ and $2$; and
ii) they are based on groupoids rather than groups. More specifically, the part $C _ { 2 } \rightarrow C _ { 1 } \underset{\rightarrow}{\rightarrow} C _ { 0 }$ is a crossed module of groupoids. An advantage of i) is that allows for crossed complexes to encode information on presentations of groups, or, through ii), of groupoids. An advantage of ii) is that it allows the modeling of cell complexes with many base points. This is necessary for modeling: the geometry of simplices; covering spaces, and in particular Cayley graphs; and the equivariant theory. It is also essential for the closed category structure on the category of crossed complexes. However, the reduced case, i.e. when $C _ { 0 }$ is a singleton, is also important.
Crossed complexes arise naturally from relative homotopy theory (cf. also Homotopy) as follows. A filtered space $X_{*}$ is a sequence $( X _ { n } ) _ { n \geq 0}$ of increasing subspaces of a space $X _ { \infty }$. One easily gets a category $\mathcal{FT} \operatorname {op}$ of filtered spaces. There is a homotopy crossed complex functor $\pi : \mathcal{FT} \text{op} \rightarrow \mathcal{C} \text{rs}$, defined using the fundamental groupoid $\pi _ { 1 } ( X _ { 1 } , X _ { 0 } )$ (cf. also Fundamental group), the relative homotopy groups $\pi _ { n } ( X _ { n } , X _ { n - 1} , x )$, $n \geq 2$, $x \in X _ { 0 }$ (cf. also Homotopy group), and appropriate boundary mappings and actions. Using geometric realization and the skeletal filtration, one gets a functor from simplicial sets to crossed complexes (cf. also Simplicial set). This has a left adjoint $N$, the nerve, and from this one gets the classifying space functor $\mathcal{B} : \mathcal{C} \text{rs} \rightarrow \mathcal{FT} \text{op}$, for which $( \mathcal{BC} ) _ { \infty }$ is called the classifying space of the crossed complex $C$ (cf. also Classifying space). There is a natural isomorphism $\pi ( \mathcal{B} C ) \cong C$, which shows that the axioms for a crossed complex are exactly the properties universally held by the topological example $\pi X_{*} $.
The category $\mathcal{C} \text{rs}$ of crossed complexes is symmetric monoidal closed (cf. also Category; Closed category; Monoid), so that for any crossed complexes $A$, $B$, $C$ there is a tensor product $A \otimes B$ and an internal Hom $\operatorname{CRS}( B , C )$ with a natural bijection $\mathcal{C}\operatorname { rs } ( A \otimes B , C ) \cong \mathcal{C}\operatorname { rs } ( A , \operatorname { CRS } ( B , C ) )$. The elements of degree $0$ and $1$ in $\operatorname{CRS}( B , C )$ are, respectively, the morphisms $B \rightarrow C$ and the homotopies of such morphisms. So one can form the set $[ B , C ]$ of homotopy classes of morphisms $B \rightarrow C$. A homotopy classification theorem is that if $X_{*}$ is the skeletal filtration of a CW-complex $X$, then there is a natural weak homotopy equivalence $B ( \operatorname{CRS} ( \pi ( X_{ * } ) , C ) ) \rightarrow ( B C ) ^ { X }$ which induces a natural bijection $[ \pi ( X _* ) , C ] \cong [ X , B C ]$. This includes results on the homotopy classification of mappings into Eilenberg–MacLane spaces, including the case of local coefficients (cf. also Eilenberg–MacLane space).
There is a generalized Van Kampen theorem [a5], stating that the functor $\pi : \mathcal{FT} \text{op} \rightarrow \mathcal{C} \text{rs}$ preserves certain colimits. This specializes to the crossed module case. It also implies the relative Hurewicz theorem (an advantage of this deduction is its generalization to the $n$-adic situation [a7]).
The proof of the generalized Van Kampen theorem given in [a5] generalizes the methods of the usual proof of the $1$-dimensional theorem, by introducing the category $\omega$-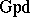 of cubical $\omega$-groupoids, and a functor $\rho : {\cal F T} \operatorname{op} \rightarrow \omega \square \operatorname{Gpd}$, together with an equivalence of categories $\gamma : \omega \square \operatorname{Gpd} \rightarrow \mathcal{C} \operatorname{rs}$ such that $\gamma \rho$ is naturally equivalent to $\pi$. Three properties of the algebraic objects $\omega$-groupoids that are necessary for the proof are:
of cubical $\omega$-groupoids, and a functor $\rho : {\cal F T} \operatorname{op} \rightarrow \omega \square \operatorname{Gpd}$, together with an equivalence of categories $\gamma : \omega \square \operatorname{Gpd} \rightarrow \mathcal{C} \operatorname{rs}$ such that $\gamma \rho$ is naturally equivalent to $\pi$. Three properties of the algebraic objects $\omega$-groupoids that are necessary for the proof are:
a) an expression for an algebraic inverse to subdivision;
b) an expression for the homotopy addition lemma;
c) a method for dealing with compositions of homotopy addition lemma situations. The proofs that $\rho ( X_{ *} )$ is an $\omega$-groupoid, i.e. is a form of higher homotopy groupoid, and is equivalent to $\pi ( X_{*} )$, are non-trivial.
There are other categories equivalent to $\mathcal{C} \text{rs}$, for example those of certain kinds of simplicial groups, and of so-called simplicial $T$-complexes, which are simplicial sets with distinguished thin elements and which are Kan complexes in a strong sense [a1] (see also Simplicial set). The latter equivalence uses the nerve functor $N$ and generalizes the so-called Dold–Kan relation between chain complexes and simplicial Abelian groups. There is also an equivalence with a category of globular $\infty$-groupoids [a6], and this shows a relation with multiple category theory [a12], p. 574. Also, the tensor product of crossed complexes corresponds to a tensor product of $\infty$-groupoids which extends for the groupoid case a tensor product of $2$-categories due to A. Gray [a12], § 6.
There is a functor from $\mathcal{C} \text{rs}$ to a category of chain complexes of modules of groupoids, and which has a right adjoint. This enables a link with classical concepts of the cohomology of groups. It also relates crossed complexes to the Fox free differential calculus defined for a presentation of a group. However, crossed complexes do carry more information than the corresponding chain complex. In particular, one can define free crossed complexes; the special case of free crossed resolutions is convenient for determining a presentation for the module of identities among relations for a presentation of a group.
The general background to the use of reduced crossed complexes and their analogues in other algebraic settings, and as a tool in non-Abelian homological algebra, is given in [a10]. This paper also shows that the use of crossed complexes to give representatives of cohomology groups $H ^ { n + 1 } ( G , A )$ of a group $G$ with coefficients in a $G$-module $A$ is a special case of results on a cohomology theory for algebras relative to a variety.
The Eilenberg–Zil'ber theorem (see Simplicial set) for the chain complex of a product $K \times L$ of simplicial sets $K$, $L$ has been generalized to a natural strong deformation retraction from $\pi ( K \times L ) \rightarrow \pi ( K ) \otimes \pi ( L )$ (cf. also Deformation retract). This allows for small models of homotopy colimits of crossed complexes.
Crossed complexes do form a closed model homotopy category in the sense of D. Quillen, but stronger results in some areas, such as equivariant theory [a4], can be obtained by constructing the appropriate homotopy coherence theory and the above homotopy colimits.
References to many of the above facts are given in [a3], [a15].
In Baues' scheme of algebraic homotopy [a2], reduced crossed complexes are called crossed chain complexes and are regarded as the linear models of pointed homotopy types. Extra quadratic information can be carried by crossed complexes $A$ with an algebra structure $A \otimes A \rightarrow A$ satisfying the usual monoid conditions. These form a non-Abelian generalization of DG-algebras. They are also a context for some notions of higher-order symmetry and for algebraic models of $3$-types.
Another generalization of crossed modules is that of crossed $n$-cubes of groups. These are remarkable for modeling all pointed, connected homotopy $n$-types. They are equivalent to certain kinds of $n$-fold groupoids [a8]. Thus, in answer to questions in the early part of the 20th century, there are higher-dimensional generalizations of the fundamental group, retaining its non-commutative nature, but which take the form of higher homotopy groupoids rather than higher homotopy groups.
Although crossed complexes form only a limited model of homotopy types, their nice formal properties as described above make them a useful tool for extending chain complex methods in a geometric and more powerful manner. This was part of the motivation for applications by J.H.C. Whitehead in combinatorial homotopy theory and simple homotopy theory [a13], [a14], which are generalized in [a2]. Whitehead's term homotopy systems for reduced free crossed complexes is also used in [a11], where applications are given to Morse theory.
References
| [a1] | N.D. Ashley, "Simplicial T-complexes: a non-abelian version of a theorem of Dold–Kan" Dissert. Math. , 165 (1988) (PhD Thesis Univ. Wales, 1976) |
| [a2] | H.-J. Baues, "Algebraic homotopy" , Cambridge Univ. Press (1989) |
| [a3] | R. Brown, "Computing homotopy types using crossed $n$-cubes of groups" N. Ray (ed.) G. Walker (ed.) , Adams Memorial Symposium on Algebraic Topology , 1 , Cambridge Univ. Press (1992) pp. 187–210 |
| [a4] | R. Brown, M. Golasinski, T. Porter, A. Tonks, "On function spaces of equivariant maps and the equivariant homotopy theory of crossed complexes" Indag. Math. , 8 (1997) pp. 157–172 |
| [a5] | R. Brown, P.J. Higgins, "Colimit theorems for relative homotopy groups" J. Pure Appl. Algebra , 22 (1981) pp. 11–41 |
| [a6] | R. Brown, P.J. Higgins, "The equivalence of $\infty$-groupoids and crossed complexes" Cah. Topol. Géom. Diff. , 22 (1981) pp. 371–386 |
| [a7] | R. Brown, J.-L. Loday, "Homotopical excision, and Hurewicz theorems, for $n$-cubes of spaces" Proc. London Math. Soc. , 54 (1987) pp. 176–192 |
| [a8] | G.J. Ellis, R. Steiner, "Higher-dimensional crossed modules and the homotopy groups of $( n + 1 )$-ads" J. Pure Appl. Algebra , 46 (1987) pp. 117–136 |
| [a9] | J. Huebschmann, "Crossed $N$-fold extensions and cohomology" Comment. Math. Helvetici , 55 (1980) pp. 302–314 |
| [a10] | A.S.-T. Lue, "Cohomology of groups relative to a variety" J. Algebra , 69 (1981) pp. 155–174 |
| [a11] | V.V. Sharko, "Functions on manifolds: Algebraic and topological aspects" , Transl. Math. Monogr. , 113 , Amer. Math. Soc. (1993) |
| [a12] | R. Street, "Categorical structures" M. Hazewinkel (ed.) , Handbook of Algebra , I , Elsevier (1996) pp. 531–577 |
| [a13] | J.H.C. Whitehead, "Combinatorial homotopy II" Bull. Amer. Math. Soc. , 55 (1949) pp. 453–496 |
| [a14] | J.H.C. Whitehead, "Simple homotopy types" Amer. J. Math. , 72 (1950) pp. 1–57 |
| [a15] | R. Brown, "Groupoids and crossed objects in algebraic topology" Homology, Homotopy and Appl. , 1 (1999) pp. 1–78 |
Crossed complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Crossed_complex&oldid=15743