Critical point
For an analytic function 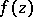 , a critical point of order
, a critical point of order 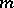 is a point
is a point  of the complex plane at which
of the complex plane at which 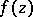 is regular but its derivative
is regular but its derivative 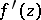 has a zero of order
has a zero of order 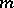 , where
, where 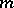 is a natural number. In other words, a critical point is defined by the conditions
is a natural number. In other words, a critical point is defined by the conditions
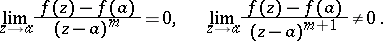 |
A critical point at infinity, 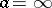 , of order
, of order 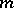 , for a function
, for a function 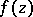 which is regular at infinity, is defined by the conditions
which is regular at infinity, is defined by the conditions
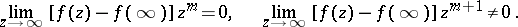 |
Under the analytic mapping 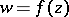 , the angle between two curves emanating from a critical point of order
, the angle between two curves emanating from a critical point of order 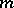 is increased by a factor
is increased by a factor 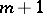 . If
. If 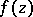 is regarded as the complex potential of some planar flow of an incompressible liquid, a critical point is characterized by the property that through it pass not one but
is regarded as the complex potential of some planar flow of an incompressible liquid, a critical point is characterized by the property that through it pass not one but 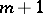 stream lines, and the velocity of the flow at a critical point vanishes. In terms of the inverse function
stream lines, and the velocity of the flow at a critical point vanishes. In terms of the inverse function 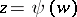 (i.e. the function for which
(i.e. the function for which 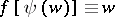 ), a critical point is an algebraic branch point of order
), a critical point is an algebraic branch point of order 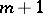 .
.
A point  of a complex
of a complex 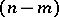 -dimensional irreducible analytic set
-dimensional irreducible analytic set
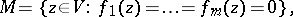 |
the latter being defined in a neighbourhood 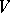 of
of  in the complex space
in the complex space 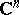 by the conditions
by the conditions 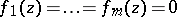 , where
, where 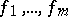 are holomorphic functions on
are holomorphic functions on 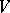 in
in  complex variables,
complex variables, 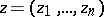 , is called a critical point if the rank of the Jacobian matrix
, is called a critical point if the rank of the Jacobian matrix 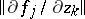 ,
,  ,
, 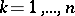 , is less than
, is less than 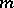 . The other points of
. The other points of 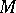 are called regular. There are relatively few critical points on
are called regular. There are relatively few critical points on  : They form an analytic set of complex dimension at most
: They form an analytic set of complex dimension at most 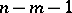 . In particular, when
. In particular, when 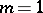 , i.e. if
, i.e. if 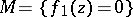 , and the dimension of
, and the dimension of 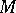 is
is 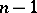 , the dimension of the set of critical points is at most
, the dimension of the set of critical points is at most  .
.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
A point as described under 2) is also called a singular point of 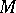 , cf. [a1].
, cf. [a1].
References
| [a1] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) pp. 95 (Translated from German) |
A critical point of a smooth (i.e. continuously differentiable) mapping 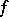 of a
of a 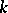 -dimensional differentiable manifold
-dimensional differentiable manifold 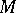 into an
into an 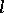 -dimensional differentiable manifold
-dimensional differentiable manifold  is a point
is a point 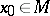 such that the rank
such that the rank 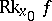 of
of 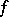 at this point (i.e. the dimension of the image
at this point (i.e. the dimension of the image 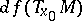 of the tangent space to
of the tangent space to 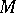 under the differential mapping
under the differential mapping 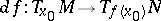 ) is less than
) is less than  . The set of all critical points is called the critical set, the image
. The set of all critical points is called the critical set, the image 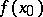 of a critical point
of a critical point 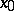 is called a critical value, and a point
is called a critical value, and a point 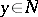 which is not the image of any critical point is called a regular point or a regular value (though it need not belong to the image
which is not the image of any critical point is called a regular point or a regular value (though it need not belong to the image 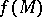 ); non-critical points of
); non-critical points of 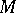 are also called regular.
are also called regular.
According to Sard's theorem, if 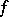 is smooth of class
is smooth of class 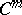 ,
, 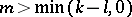 , then the image of the critical set is of the first category in
, then the image of the critical set is of the first category in 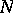 (i.e. it is the union of at most countably many nowhere-dense sets) and has
(i.e. it is the union of at most countably many nowhere-dense sets) and has 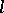 -dimensional measure zero (see [1], [2]). The lower bound for
-dimensional measure zero (see [1], [2]). The lower bound for 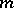 cannot be weakened (see [3]). The case most frequently needed is
cannot be weakened (see [3]). The case most frequently needed is 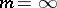 (in which case the proof is simplified, see [4]). This theorem is widely used for reductions to general position via "small movements" ; for example, it may readily be used to prove that, given two smooth submanifolds in
(in which case the proof is simplified, see [4]). This theorem is widely used for reductions to general position via "small movements" ; for example, it may readily be used to prove that, given two smooth submanifolds in 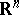 , there exists an arbitrarily small translation of one of them such that their intersection will also be a submanifold (see [2], [4], and also Transversality of mappings).
, there exists an arbitrarily small translation of one of them such that their intersection will also be a submanifold (see [2], [4], and also Transversality of mappings).
According to the above definition, when 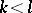 every point
every point 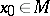 must be considered as critical. Then, however, there are considerable differences between the properties of the points
must be considered as critical. Then, however, there are considerable differences between the properties of the points 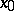 for which
for which 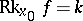 and the points for which
and the points for which 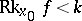 . In the former case there is a neighbourhood of
. In the former case there is a neighbourhood of 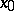 in which the mapping
in which the mapping 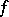 looks roughly like the standard imbedding of
looks roughly like the standard imbedding of 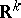 into
into 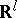 ; more precisely, there exist local coordinates
; more precisely, there exist local coordinates  near
near 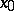 (on
(on 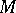 ) and
) and 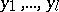 near
near 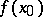 (on
(on 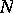 ), in terms of which
), in terms of which 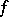 is given by
is given by
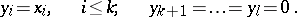 |
In the second case the image of a neighbourhood of 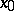 need not be a manifold, displaying instead various singularities — cusps, self-intersections, etc. For this reason, the definition of a critical point is often modified to include only points
need not be a manifold, displaying instead various singularities — cusps, self-intersections, etc. For this reason, the definition of a critical point is often modified to include only points 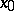 such that
such that 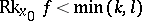 ; corresponding modifications are then necessary in the definitions of the other terms listed above [5].
; corresponding modifications are then necessary in the definitions of the other terms listed above [5].
The behaviour of mappings in a neighbourhood of a critical point is investigated in the theory of singularities of differentiable mappings (see [5], [6]). In that context one studies not arbitrary critical points (concerning which little can be said), but critical points satisfying conditions which ensure that they are "not too strongly degenerate" and "typical" . Thus, one considers critical points of sufficiently smooth mappings, or families of mappings (which depend smoothly on finitely many parameters), which are "unremovable" in the sense that, under small perturbations ( "small" being understood in the sense of  for suitable
for suitable  ) of the original mapping, or of the original family, the perturbed mapping (family) has a critical point of the same type in some neighbourhood of the original critical point. For a mapping
) of the original mapping, or of the original family, the perturbed mapping (family) has a critical point of the same type in some neighbourhood of the original critical point. For a mapping 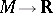 (i.e. an ordinary scalar function; in this case critical points are often called stationary points), critical points which are typical in the indicated sense are the non-degenerate critical points at which the Hessian is a non-degenerate quadratic form. Concerning typical critical points for a family of functions see [6], [7].
(i.e. an ordinary scalar function; in this case critical points are often called stationary points), critical points which are typical in the indicated sense are the non-degenerate critical points at which the Hessian is a non-degenerate quadratic form. Concerning typical critical points for a family of functions see [6], [7].
References
| [1] | A. Sard, "The measure of critical values of differentiable maps" Bull. Amer. Math Soc. , 48 (1942) pp. 883–890 |
| [2] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [3] | H. Whitney, "A function not constant on a connected set of critical points" Duke Math. J. , 1 : 4 (1935) pp. 514–517 |
| [4] | J.W. Milnor, "Topology from the differential viewpoint" , Univ. Virginia Press (1965) |
| [5] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1974) |
| [6] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) |
| [7] | V.I. Arnol'd, "Normal forms of functions near degenerate critical points, the Weyl groups 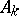 , , 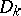 , , 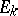 and Lagrangian singularities" Funktsional. Anal. i Prilozh. , 6 : 4 (1972) pp. 3–25 (In Russian) and Lagrangian singularities" Funktsional. Anal. i Prilozh. , 6 : 4 (1972) pp. 3–25 (In Russian) |
D.V. Anosov
Critical point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Critical_point&oldid=16181