Critical function

A statistic for which the values are the conditional probabilities of the deviations from the hypothesis being tested, given the value of an observed result. Let be a random variable with values in a sample space , the distribution of which belongs to a family , and suppose one is testing the hypothesis : , against the alternative : . Let be a measurable function on such that for all 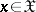. If the hypothesis is being tested by a randomized test, according to which is rejected with probability 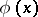if the experiment reveals that 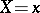, and accepted with probability , then 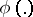is called the critical function of the test. In setting up a non-randomized test, one chooses the critical function in such a way that it assumes only two values, 0 and 1. 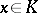Hence it is the characteristic function of a certain set , called the critical region of the test: if , if .

References

[1]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959)