Creative set
A recursively enumerable set 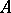 of natural numbers whose complement
of natural numbers whose complement 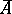 (in the set of natural numbers) is a productive set; in other words, a set
(in the set of natural numbers) is a productive set; in other words, a set 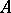 is creative if it is recursively enumerable and if there exists a partial recursive function
is creative if it is recursively enumerable and if there exists a partial recursive function 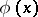 such that, for any recursively enumerable subset
such that, for any recursively enumerable subset 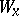 in
in 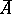 , with Gödel number
, with Gödel number  ,
,
 |
Creative sets are frequently encountered in various algorithmically unsolvable problems, and they therefore constitute the most important class of recursively enumerable sets which are not recursive. In many formal theories, the sets of (numbers of) provable and refutable formulas turn out to be creative (assuming a natural enumeration of all formulas of the theory); in particular, this is the case for Peano arithmetic and, in general, for all recursively inseparable theories (i.e. theories the sets of provable and refutable formulas of which are effectively inseparable). All creative sets are recursively isomorphic to one another (i.e. for any two creative sets there exists a recursive one-to-one mapping of the natural numbers which maps one set onto the other), and they all belong to the same Turing degree — the largest of the degrees of recursively enumerable sets. The concept of creativity generalizes to sequences of sets and other objects.
References
| [1] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) |
| [2] | J.R. Shoenfield, "Mathematical logic" , Addison-Wesley (1967) |
Comments
For definitions and discussions of the various concepts mentioned above, such as recursively enumerable set, recursive isomorphism, Turing degree, etc. cf. Recursive set theory and Degree of undecidability.
Creative set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Creative_set&oldid=13027