Difference between revisions of "Coxeter group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | c0269801.png | ||
| + | $#A+1 = 91 n = 1 | ||
| + | $#C+1 = 91 : ~/encyclopedia/old_files/data/C026/C.0206980 Coxeter group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | where | + | A group with a distinguished system of generators $ \{ {r _ {i} } : {i \in I } \} $ |
| + | admitting a system of defining relations | ||
| + | |||
| + | $$ | ||
| + | ( r _ {i} r _ {j} ) ^ {n _ {ij} } = 1 ,\ \ | ||
| + | i , j \in I , | ||
| + | $$ | ||
| + | |||
| + | where $ n _ {ii} = 1 $( | ||
| + | so that $ r _ {i} ^ {2} = 1 $ | ||
| + | for any $ i $) | ||
| + | and $ n _ {ij} = n _ {ji} $( | ||
| + | for $ i \neq j $) | ||
| + | is an integer $ \geq 2 $ | ||
| + | or equal to $ \infty $( | ||
| + | in the latter case there is no relation between $ r _ {i} $ | ||
| + | and $ r _ {j} $). | ||
| + | Under these conditions $ n _ {ij} $ | ||
| + | is the same as the order of the element $ r _ {i} r _ {j} $. | ||
| + | If $ n _ {ij} = 2 $, | ||
| + | then $ r _ {i} $ | ||
| + | and $ r _ {j} $ | ||
| + | commute. The matrix $ ( n _ {ij} ) _ {i , j \in I } $ | ||
| + | is called the Coxeter matrix of the given Coxeter group. The matrix (and therefore the group) can be given by means of the Coxeter graph, which is the graph with vertices $ a _ {i} $( | ||
| + | $ i \in I $) | ||
| + | in which $ a _ {i} $ | ||
| + | and $ a _ {j} $ | ||
| + | are joined by an $ ( n _ {ij} - 2 ) $- | ||
| + | fold edge if $ n _ {ij} < \infty $( | ||
| + | in particular, they are not joined if $ n _ {ij} = 2 $), | ||
| + | and are joined by a thick edge if $ n _ {ij} = \infty $. | ||
| + | In an alternative notation, the vertices $ a _ {i} $ | ||
| + | and $ a _ {j} $ | ||
| + | of the Coxeter graph are joined by a simple edge with label $ n _ {ij} $. | ||
===Examples.=== | ===Examples.=== | ||
| − | + | 1) Every group generated by two elements of order $ 2 $ | |
| − | 1) Every group generated by two elements of order | + | is a Coxeter group with graph |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026980a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026980a.gif" /> | ||
| Line 14: | Line 55: | ||
Figure: c026980a | Figure: c026980a | ||
| − | where | + | where $ m $ |
| + | is the half the order of the group. | ||
| − | 2) The symmetric group | + | 2) The symmetric group $ S _ {n} $ |
| + | is a Coxeter group with respect to the generators $ r _ {i} = ( i , i + 1 ) $, | ||
| + | $ i = 1 \dots n - 1 $; | ||
| + | its Coxeter graph has the form | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026980b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026980b.gif" /> | ||
| Line 22: | Line 67: | ||
Figure: c026980b | Figure: c026980b | ||
| − | 3) The group | + | 3) The group $ \mathop{\rm PGL} _ {2} ( \mathbf Z ) = \mathop{\rm GL} _ {2} ( \mathbf Z ) / \{ \pm 1 \} $ |
| + | is a Coxeter group with respect to the generators | ||
| − | + | $$ | |
| + | r _ {1} = \left \{ \pm | ||
| + | \left \| | ||
| + | \begin{array}{rc} | ||
| + | - 1 & 0 \\ | ||
| + | 0 & 1 \\ | ||
| + | \end{array} | ||
| + | \right \| \right \} ,\ \ | ||
| + | r _ {2} = \ | ||
| + | \left \{ \pm | ||
| + | \left \| | ||
| + | \begin{array}{rc} | ||
| + | - 1 & 0 \\ | ||
| + | 1 & 1 \\ | ||
| + | \end{array} | ||
| + | \right \| \right \} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | r _ {3} = \left \{ \pm \left \| | ||
| + | \begin{array}{cr} | ||
| + | 0 &- 1 \\ | ||
| + | 1 & 0 \\ | ||
| + | \end{array} | ||
| + | \right \| \right \} ; | ||
| + | $$ | ||
its graph has the form | its graph has the form | ||
| Line 34: | Line 103: | ||
Figure: c026980c | Figure: c026980c | ||
| − | The group | + | The group $ \mathop{\rm PGL} _ {2} ( \mathbf Z ) $ |
| + | contains the subgroup $ \mathop{\rm PSL} _ {2} ( \mathbf Z ) = \mathop{\rm SL} _ {2} ( \mathbf Z ) / \{ \pm 1 \} $ | ||
| + | of index $ 2 $, | ||
| + | isomorphic to the modular Kleinian group. | ||
The notion of a Coxeter group arose in the theory of discrete groups generated by hyperplane reflections (see [[Reflection group|Reflection group]]). | The notion of a Coxeter group arose in the theory of discrete groups generated by hyperplane reflections (see [[Reflection group|Reflection group]]). | ||
| Line 40: | Line 112: | ||
Every reflection group is a Coxeter group, if one takes as generators the reflections in the hyperplanes that bound its fundamental polyhedron. Included among the reflection groups are the Weyl groups (ordinary and affine) of semi-simple Lie groups (cf. [[Weyl group|Weyl group]]). | Every reflection group is a Coxeter group, if one takes as generators the reflections in the hyperplanes that bound its fundamental polyhedron. Included among the reflection groups are the Weyl groups (ordinary and affine) of semi-simple Lie groups (cf. [[Weyl group|Weyl group]]). | ||
| − | In 1934 H.S.M. Coxeter [[#References|[1]]] enumerated all the reflection groups in an | + | In 1934 H.S.M. Coxeter [[#References|[1]]] enumerated all the reflection groups in an $ n $- |
| + | dimensional Euclidean space $ E ^ {n} $ | ||
| + | and proved that they are all Coxeter groups, as they are now called. In his next paper [[#References|[2]]], he proved that every finite Coxeter group is isomorphic to some reflection group in $ E ^ {n} $ | ||
| + | whose elements have a common fixed point, and so obtained a classification of the finite Coxeter groups (see Table 1).<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">Designation of the group</td> <td colname="2" style="background-color:white;" colspan="1">Its Coxeter graph</td> <td colname="3" style="background-color:white;" colspan="1">Its exponents</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {n} , n \geq 1 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 \dots n $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ B _ {n} \textrm{ or } C _ {n} , n \geq 2 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 3 \dots 2n- 1 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ D _ {n} , n\geq 4 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 3 \dots 2n- 3 , n- 1 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {6} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 4, 5, 7 , 8 , 11 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {7} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 5, 7 , 9 , 11 , 13 , 17 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {8} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 7 , 11 , 13 , 17 , 19 , 23 , 29 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ F _ {4} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 5 , 7 , 11 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ G _ {2} ^ {(} m) , m\geq 5 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , m- 1 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ H _ {3} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 5 , 9 $ |
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ H _ {4} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> <td colname="3" style="background-color:white;" colspan="1"> | + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ 1 , 11 , 19 , 28 $ |
| + | </td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | Among the infinite Coxeter groups one distinguishes the affine and hyperbolic Coxeter groups. A Coxeter group is affine (or hyperbolic) if it is isomorphic to a reflection group in | + | Among the infinite Coxeter groups one distinguishes the affine and hyperbolic Coxeter groups. A Coxeter group is affine (or hyperbolic) if it is isomorphic to a reflection group in $ E ^ {n} $( |
| + | or in the Lobachevskii space $ L ^ {n} $) | ||
| + | whose elements have no common invariant subspace of dimension $ < n $( | ||
| + | in the hyperbolic case, the point at infinity also has to be considered to be a subspace).<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">Designation of the group</td> <td colname="2" style="background-color:white;" colspan="1">Its Coxeter graph</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{A} _ {1} $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{A} _ {n} , n \geq 2 $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{B} _ {n} , n \geq 3 $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{C} _ {n} , n\geq 2 $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{D} _ {n} , n \geq 4 $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{E} _ {6} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{E} _ {7} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{E} _ {8} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{F} _ {4} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \widetilde{G} _ {2} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| Line 130: | Line 238: | ||
The affine Coxeter groups have been enumerated by Coxeter (see Table. 2); they arise in the theory of semi-simple Lie groups as affine Weyl groups. | The affine Coxeter groups have been enumerated by Coxeter (see Table. 2); they arise in the theory of semi-simple Lie groups as affine Weyl groups. | ||
| − | A Coxeter group with | + | A Coxeter group with $ k $ |
| + | generators is a two-dimensional hyperbolic Coxeter group if and only if, under a suitable numbering of the generators, | ||
| − | + | $$ | |
| − | and | + | \frac{1}{n _ {12} } |
| + | + | ||
| + | \frac{1}{n _ {23} } | ||
| + | + \dots + | ||
| + | \frac{1}{n _ {k1} } | ||
| + | < 1 | ||
| + | $$ | ||
| + | |||
| + | and $ n _ {ij} = \infty $ | ||
| + | when $ | i - j | > 1 $. | ||
| + | With regard to $ n $- | ||
| + | dimensional hyperbolic Coxeter groups with $ n > 2 $, | ||
| + | a complete enumeration of them is not considered possible, although definite success has been achieved in the study of the more important classes of such groups (see [[Reflection group|Reflection group]]). | ||
The finite, affine and hyperbolic Coxeter groups and the direct products of these constitute only a small fraction of the Coxeter groups. An arbitrary Coxeter group with a finite number of generators admits a finite-dimensional real linear representation, as was shown explicitly by Coxeter [[#References|[2]]], under which the generators are mapped onto linear reflections. It has been proved [[#References|[4]]] that this representation is faithful, which implies, in particular, the solution of the word problem in Coxeter groups [[#References|[5]]]. | The finite, affine and hyperbolic Coxeter groups and the direct products of these constitute only a small fraction of the Coxeter groups. An arbitrary Coxeter group with a finite number of generators admits a finite-dimensional real linear representation, as was shown explicitly by Coxeter [[#References|[2]]], under which the generators are mapped onto linear reflections. It has been proved [[#References|[4]]] that this representation is faithful, which implies, in particular, the solution of the word problem in Coxeter groups [[#References|[5]]]. | ||
==Parabolic subgroups of a Coxeter group.== | ==Parabolic subgroups of a Coxeter group.== | ||
| − | Let | + | Let $ G $ |
| + | be a Coxeter group with system of generators $ \{ {r _ {i} } : {i \in I } \} $. | ||
| + | For any subset $ J \subset I $, | ||
| + | the subgroup $ G _ {J} $ | ||
| + | generated by the set $ \{ {r _ {i} } : {i \in J } \} $ | ||
| + | is a Coxeter group, where $ r _ {i} \notin G _ {J} $ | ||
| + | when $ i \notin J $. | ||
| + | A subgroup of this form is called parabolic. | ||
| − | A Coxeter group is called indecomposable if it is not a direct product of two non-trivial standard subgroups; this is equivalent to the connectedness of its Coxeter graph. All finite (or affine) Coxeter groups are direct products of indecomposable Coxeter groups of the same type; all hyperbolic Coxeter groups are indecomposable. An indecomposable Coxeter group is finite (respectively, affine, hyperbolic) if and only if the symmetric matrix | + | A Coxeter group is called indecomposable if it is not a direct product of two non-trivial standard subgroups; this is equivalent to the connectedness of its Coxeter graph. All finite (or affine) Coxeter groups are direct products of indecomposable Coxeter groups of the same type; all hyperbolic Coxeter groups are indecomposable. An indecomposable Coxeter group is finite (respectively, affine, hyperbolic) if and only if the symmetric matrix $ \| - \cos ( \pi / n _ {ij} ) \| $ |
| + | is positive definite (respectively, positive semi-definite, has rank at least $ | I | - 1 $ | ||
| + | and has negative index $ 1 $). | ||
In the theory of finite Coxeter groups, an important role is played by their so-called exponents (see Table 1); these are one less than the degrees of the generating invariants of the corresponding reflection group. One can express in terms of exponents the order of the group, the number of reflections (elements conjugate to the generators), etc., see [[Reflection group|Reflection group]]. | In the theory of finite Coxeter groups, an important role is played by their so-called exponents (see Table 1); these are one less than the degrees of the generating invariants of the corresponding reflection group. One can express in terms of exponents the order of the group, the number of reflections (elements conjugate to the generators), etc., see [[Reflection group|Reflection group]]. | ||
| Line 149: | Line 279: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H.S.M. Coxeter, "Discrete groups generated by reflections" ''Ann. of Math.'' , '''35''' (1934) pp. 588–621</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.S.M. Coxeter, "The complete enumeration of finite groups of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026980/c02698092.png" />" ''J. London Math. Soc.'' , '''10''' (1935) pp. 21–25</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H.S.M. Coxeter, "The product of generators of a finite group generated by reflections" ''Duke Math. J.'' , '''18''' (1951) pp. 765–782</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Tits, "Le problème des mots dans les groupes de Coxeter" , ''Symp. Math.'' , '''1''' , Acad. Press (1969) pp. 175–185</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H.S.M. Coxeter, "Discrete groups generated by reflections" ''Ann. of Math.'' , '''35''' (1934) pp. 588–621</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.S.M. Coxeter, "The complete enumeration of finite groups of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026980/c02698092.png" />" ''J. London Math. Soc.'' , '''10''' (1935) pp. 21–25</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H.S.M. Coxeter, "The product of generators of a finite group generated by reflections" ''Duke Math. J.'' , '''18''' (1951) pp. 765–782</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Tits, "Le problème des mots dans les groupes de Coxeter" , ''Symp. Math.'' , '''1''' , Acad. Press (1969) pp. 175–185</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
The diagrams occurring in Tables 1 and 2 in the Western literature are usually called Dynkin diagrams, particularly in the context of the corresponding simple finite-dimensional Lie algebras and the corresponding affine Kac–Moody algebras (Kac–Moody Lie algebras), cf., e.g., [[#References|[4]]]. | The diagrams occurring in Tables 1 and 2 in the Western literature are usually called Dynkin diagrams, particularly in the context of the corresponding simple finite-dimensional Lie algebras and the corresponding affine Kac–Moody algebras (Kac–Moody Lie algebras), cf., e.g., [[#References|[4]]]. | ||
Revision as of 17:31, 5 June 2020
A group with a distinguished system of generators $ \{ {r _ {i} } : {i \in I } \} $
admitting a system of defining relations
$$ ( r _ {i} r _ {j} ) ^ {n _ {ij} } = 1 ,\ \ i , j \in I , $$
where $ n _ {ii} = 1 $( so that $ r _ {i} ^ {2} = 1 $ for any $ i $) and $ n _ {ij} = n _ {ji} $( for $ i \neq j $) is an integer $ \geq 2 $ or equal to $ \infty $( in the latter case there is no relation between $ r _ {i} $ and $ r _ {j} $). Under these conditions $ n _ {ij} $ is the same as the order of the element $ r _ {i} r _ {j} $. If $ n _ {ij} = 2 $, then $ r _ {i} $ and $ r _ {j} $ commute. The matrix $ ( n _ {ij} ) _ {i , j \in I } $ is called the Coxeter matrix of the given Coxeter group. The matrix (and therefore the group) can be given by means of the Coxeter graph, which is the graph with vertices $ a _ {i} $( $ i \in I $) in which $ a _ {i} $ and $ a _ {j} $ are joined by an $ ( n _ {ij} - 2 ) $- fold edge if $ n _ {ij} < \infty $( in particular, they are not joined if $ n _ {ij} = 2 $), and are joined by a thick edge if $ n _ {ij} = \infty $. In an alternative notation, the vertices $ a _ {i} $ and $ a _ {j} $ of the Coxeter graph are joined by a simple edge with label $ n _ {ij} $.
Examples.
1) Every group generated by two elements of order $ 2 $ is a Coxeter group with graph

Figure: c026980a
where $ m $ is the half the order of the group.
2) The symmetric group $ S _ {n} $ is a Coxeter group with respect to the generators $ r _ {i} = ( i , i + 1 ) $, $ i = 1 \dots n - 1 $; its Coxeter graph has the form

Figure: c026980b
3) The group $ \mathop{\rm PGL} _ {2} ( \mathbf Z ) = \mathop{\rm GL} _ {2} ( \mathbf Z ) / \{ \pm 1 \} $ is a Coxeter group with respect to the generators
$$ r _ {1} = \left \{ \pm \left \| \begin{array}{rc} - 1 & 0 \\ 0 & 1 \\ \end{array} \right \| \right \} ,\ \ r _ {2} = \ \left \{ \pm \left \| \begin{array}{rc} - 1 & 0 \\ 1 & 1 \\ \end{array} \right \| \right \} , $$
$$ r _ {3} = \left \{ \pm \left \| \begin{array}{cr} 0 &- 1 \\ 1 & 0 \\ \end{array} \right \| \right \} ; $$
its graph has the form

Figure: c026980c
The group $ \mathop{\rm PGL} _ {2} ( \mathbf Z ) $ contains the subgroup $ \mathop{\rm PSL} _ {2} ( \mathbf Z ) = \mathop{\rm SL} _ {2} ( \mathbf Z ) / \{ \pm 1 \} $ of index $ 2 $, isomorphic to the modular Kleinian group.
The notion of a Coxeter group arose in the theory of discrete groups generated by hyperplane reflections (see Reflection group).
Every reflection group is a Coxeter group, if one takes as generators the reflections in the hyperplanes that bound its fundamental polyhedron. Included among the reflection groups are the Weyl groups (ordinary and affine) of semi-simple Lie groups (cf. Weyl group).
In 1934 H.S.M. Coxeter [1] enumerated all the reflection groups in an $ n $- dimensional Euclidean space $ E ^ {n} $ and proved that they are all Coxeter groups, as they are now called. In his next paper [2], he proved that every finite Coxeter group is isomorphic to some reflection group in $ E ^ {n} $
whose elements have a common fixed point, and so obtained a classification of the finite Coxeter groups (see Table 1).
<tbody> </tbody>
|
Among the infinite Coxeter groups one distinguishes the affine and hyperbolic Coxeter groups. A Coxeter group is affine (or hyperbolic) if it is isomorphic to a reflection group in $ E ^ {n} $( or in the Lobachevskii space $ L ^ {n} $) whose elements have no common invariant subspace of dimension $ < n $(
in the hyperbolic case, the point at infinity also has to be considered to be a subspace).
<tbody> </tbody>
|
The affine Coxeter groups have been enumerated by Coxeter (see Table. 2); they arise in the theory of semi-simple Lie groups as affine Weyl groups.
A Coxeter group with $ k $ generators is a two-dimensional hyperbolic Coxeter group if and only if, under a suitable numbering of the generators,
$$ \frac{1}{n _ {12} } + \frac{1}{n _ {23} } + \dots + \frac{1}{n _ {k1} } < 1 $$
and $ n _ {ij} = \infty $ when $ | i - j | > 1 $. With regard to $ n $- dimensional hyperbolic Coxeter groups with $ n > 2 $, a complete enumeration of them is not considered possible, although definite success has been achieved in the study of the more important classes of such groups (see Reflection group).
The finite, affine and hyperbolic Coxeter groups and the direct products of these constitute only a small fraction of the Coxeter groups. An arbitrary Coxeter group with a finite number of generators admits a finite-dimensional real linear representation, as was shown explicitly by Coxeter [2], under which the generators are mapped onto linear reflections. It has been proved [4] that this representation is faithful, which implies, in particular, the solution of the word problem in Coxeter groups [5].
Parabolic subgroups of a Coxeter group.
Let $ G $ be a Coxeter group with system of generators $ \{ {r _ {i} } : {i \in I } \} $. For any subset $ J \subset I $, the subgroup $ G _ {J} $ generated by the set $ \{ {r _ {i} } : {i \in J } \} $ is a Coxeter group, where $ r _ {i} \notin G _ {J} $ when $ i \notin J $. A subgroup of this form is called parabolic.
A Coxeter group is called indecomposable if it is not a direct product of two non-trivial standard subgroups; this is equivalent to the connectedness of its Coxeter graph. All finite (or affine) Coxeter groups are direct products of indecomposable Coxeter groups of the same type; all hyperbolic Coxeter groups are indecomposable. An indecomposable Coxeter group is finite (respectively, affine, hyperbolic) if and only if the symmetric matrix $ \| - \cos ( \pi / n _ {ij} ) \| $ is positive definite (respectively, positive semi-definite, has rank at least $ | I | - 1 $ and has negative index $ 1 $).
In the theory of finite Coxeter groups, an important role is played by their so-called exponents (see Table 1); these are one less than the degrees of the generating invariants of the corresponding reflection group. One can express in terms of exponents the order of the group, the number of reflections (elements conjugate to the generators), etc., see Reflection group.
The product of all the generators of a finite Coxeter group, up to conjugacy, does not depend on the order of multiplication and is called the Killing–Coxeter element or Coxeter element [3].
References
| [1] | H.S.M. Coxeter, "Discrete groups generated by reflections" Ann. of Math. , 35 (1934) pp. 588–621 |
| [2] | H.S.M. Coxeter, "The complete enumeration of finite groups of the form 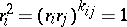 " J. London Math. Soc. , 10 (1935) pp. 21–25 " J. London Math. Soc. , 10 (1935) pp. 21–25 |
| [3] | H.S.M. Coxeter, "The product of generators of a finite group generated by reflections" Duke Math. J. , 18 (1951) pp. 765–782 |
| [4] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [5] | J. Tits, "Le problème des mots dans les groupes de Coxeter" , Symp. Math. , 1 , Acad. Press (1969) pp. 175–185 |
Comments
The diagrams occurring in Tables 1 and 2 in the Western literature are usually called Dynkin diagrams, particularly in the context of the corresponding simple finite-dimensional Lie algebras and the corresponding affine Kac–Moody algebras (Kac–Moody Lie algebras), cf., e.g., [4].
Coxeter group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coxeter_group&oldid=15082