absolute differentiation
An operation that defines in an invariant way the notions of a derivative and a differential for fields of geometric objects on manifolds, such as vectors, tensors, forms, etc. The basic concepts of the theory of covariant differentiation were given (under the name of absolute differential calculus) at the end of the 19th century in papers by G. Ricci, and in its most complete form in 1901 by him in collaboration with T. Levi-Civita (see [1]). At first, the theory of covariant differentiation was constructed on Riemannian manifolds and was intended in the first instance for the investigation of the invariants of differential forms. The definition and properties of covariant differentiation subsequently proved to be related in a natural way with the notions of connection and parallel displacement on manifolds, which were introduced later. Nowadays the theory of covariant differentiation is developed within the general framework of the theory of connections. As a device of tensor analysis, covariant differentiation is widely used in theoretical physics, particularly in the general theory of relativity.
Let an affine connection be given on an  -dimensional manifold
-dimensional manifold 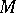 as well as the parallel displacement of vectors and, more generally, tensors, associated with it. Let
as well as the parallel displacement of vectors and, more generally, tensors, associated with it. Let 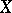 be a smooth vector field,
be a smooth vector field, 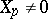 ,
, 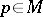 , and let
, and let 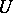 be a tensor field of type
be a tensor field of type 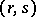 , that is,
, that is,  times contravariant and
times contravariant and  times covariant; by the covariant derivative (with respect to the given connection) of
times covariant; by the covariant derivative (with respect to the given connection) of 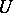 at
at 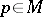 along
along 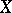 one means the tensor (of the same type
one means the tensor (of the same type 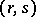 )
)
 |
where 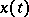 is the point on the integral curve
is the point on the integral curve 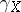 of the vector field
of the vector field 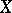 with initial condition
with initial condition 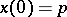 ,
, 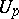 and
and 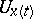 are, respectively, the localizations (values) of
are, respectively, the localizations (values) of 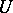 at
at 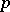 and
and 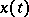 , and
, and 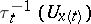 is the result of the parallel displacement of
is the result of the parallel displacement of 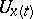 along
along 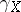 from
from 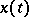 to
to 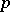 . Thus the basic idea behind the definition of the covariant derivative of a tensor field
. Thus the basic idea behind the definition of the covariant derivative of a tensor field 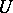 along a vector field
along a vector field 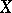 is that, in view of the absence of a natural relation between
is that, in view of the absence of a natural relation between 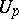 and
and 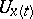 , as they belong to different fibres of the tensor bundle over
, as they belong to different fibres of the tensor bundle over 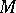 , that is, they are in tensor spaces
, that is, they are in tensor spaces 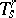 over different tangent spaces
over different tangent spaces 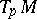 and
and 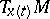 to
to 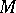 , the difference between
, the difference between 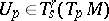 and the image of
and the image of 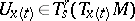 under the parallel displacement along
under the parallel displacement along 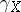 to
to 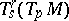 serves as the "increment" of
serves as the "increment" of 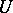 ; one then takes the limit of the ratio of this "increment" to the increment of the argument
; one then takes the limit of the ratio of this "increment" to the increment of the argument 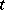 in the usual way. If, in particular, for points
in the usual way. If, in particular, for points 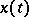 near to
near to 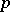 the field
the field 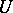 is obtained by parallel displacement of the tensor
is obtained by parallel displacement of the tensor 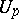 along
along 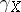 , then
, then 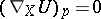 , and therefore, in general, the covariant derivative of
, and therefore, in general, the covariant derivative of 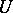 at
at 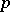 along
along 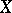 defines the initial rate of the difference of
defines the initial rate of the difference of 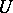 along
along 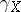 from the result of the parallel displacement of
from the result of the parallel displacement of 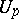 along
along 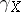 . For tensor fields of zero valency, that is, for functions
. For tensor fields of zero valency, that is, for functions 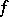 in the ring
in the ring 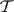 of differentiable functions on
of differentiable functions on 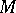 ,
,
 |
which leads to the identification of 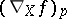 with the derivative of
with the derivative of 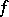 along the vector
along the vector 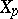 , that is, with
, that is, with 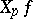 . When
. When 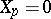 one has, by definition,
one has, by definition, 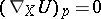 for any tensor field
for any tensor field 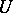 .
.
The introduction of a covariant derivative enables one to define the covariant differential 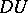 of a tensor field
of a tensor field 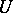 along a smooth curve
along a smooth curve 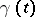 as
as
which can be regarded as the principal linear part of the "increment" of 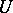 (in the sense described above) under the displacement along
(in the sense described above) under the displacement along 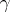 of the point by an infinitesimal segment
of the point by an infinitesimal segment 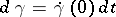 .
.
The knowledge of 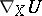 for a tensor field
for a tensor field 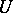 of type
of type 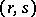 at each point
at each point 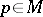 along each vector field
along each vector field 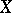 enables one to introduce for
enables one to introduce for 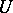 : 1) the covariant differential field
: 1) the covariant differential field 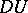 as a tensor
as a tensor 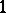 -form with values in the module
-form with values in the module 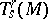 , defined on the vectors of
, defined on the vectors of 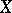 by the formula
by the formula 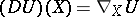 ; 2) the covariant derivative field
; 2) the covariant derivative field 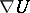 as a tensor field of type
as a tensor field of type 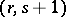 , corresponding canonically to the form
, corresponding canonically to the form 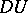 and acting on
and acting on 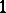 -forms
-forms 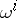 and vectors
and vectors 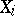 according to the formula
according to the formula
By the covariant differential one usually means not the 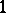 -form
-form 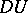 itself but its values at the vectors
itself but its values at the vectors 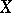 , and in this interpretation
, and in this interpretation 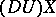 is also converted into a tensor field of type
is also converted into a tensor field of type 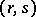 the localization of which, in particular, when
the localization of which, in particular, when 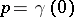 and
and 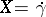 , is the same as the covariant differential
, is the same as the covariant differential 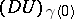 along the curve
along the curve 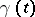 , introduced above. The covariant derivative
, introduced above. The covariant derivative 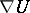 is sometimes called the gradient of the tensor
is sometimes called the gradient of the tensor 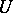 and the derivative, the covariant differential.
and the derivative, the covariant differential.
If 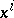 are local coordinates,
are local coordinates, 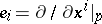 denotes the corresponding basis of the space of vector fields,
denotes the corresponding basis of the space of vector fields, 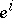 denotes the dual basis for the space of
denotes the dual basis for the space of 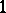 -forms,
-forms, 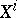 and
and 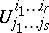 are the coordinates of vector and tensor fields in these bases, and
are the coordinates of vector and tensor fields in these bases, and 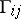 are the coefficients of an affine connection introduced on the manifold
are the coefficients of an affine connection introduced on the manifold 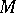 (cf. Linear connection), then, denoting by
(cf. Linear connection), then, denoting by 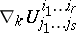 or
or 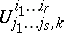 the components of the tensor field
the components of the tensor field 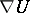 , one obtains the following expressions (as an example,
, one obtains the following expressions (as an example, 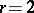 ,
, 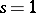 have been chosen):
have been chosen):
where 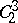 is the operation of contraction (cf. Contraction of a tensor) with respect to the third contravariant and second covariant indices.
is the operation of contraction (cf. Contraction of a tensor) with respect to the third contravariant and second covariant indices.
If 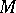 is an affine space and
is an affine space and 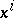 are affine coordinates, then
are affine coordinates, then 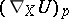 is the ordinary derivative of the tensor field
is the ordinary derivative of the tensor field 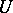 along the vector field
along the vector field 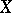 , the
, the 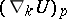 are the partial derivatives of
are the partial derivatives of 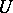 at
at 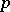 with respect to
with respect to 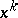 , and
, and 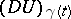 is the ordinary differential of
is the ordinary differential of 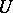 along the curve
along the curve 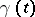 . Thus the covariant derivative emerges as a generalization of ordinary differentiation for which the well-known relationships between the first-order partial derivatives and differentials remain valid.
. Thus the covariant derivative emerges as a generalization of ordinary differentiation for which the well-known relationships between the first-order partial derivatives and differentials remain valid.
The value of covariant differentiation is that it provides a convenient analytic apparatus for the study and description of the properties of geometric objects and operations in invariant form. For example, the condition for parallel displacement of a tensor 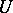 along a curve
along a curve 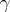 is given by the equation
is given by the equation 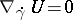 , the equation of a geodesic
, the equation of a geodesic 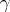 is written in the form
is written in the form 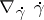 , the integrability condition for a system of equations in covariant derivatives of the first order is reduced to an equation for the alternating difference
, the integrability condition for a system of equations in covariant derivatives of the first order is reduced to an equation for the alternating difference 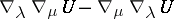 ; exterior differentiation of forms on a manifold and in bundles over it can also be expressed in terms of covariant differentiation; and there are other examples.
; exterior differentiation of forms on a manifold and in bundles over it can also be expressed in terms of covariant differentiation; and there are other examples.
The definition of higher covariant derivatives is given inductively: 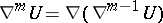 . Generally speaking, the tensor
. Generally speaking, the tensor 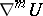 obtained in this way is not symmetric in the last covariant indices; higher covariant derivatives along different vector fields also depend on the order of differentiation. The alternating differences of the covariant derivatives of higher orders are expressed in terms of the curvature tensor
obtained in this way is not symmetric in the last covariant indices; higher covariant derivatives along different vector fields also depend on the order of differentiation. The alternating differences of the covariant derivatives of higher orders are expressed in terms of the curvature tensor 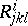 and torsion tensor
and torsion tensor 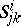 , which together characterize the difference between the manifold
, which together characterize the difference between the manifold 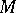 and affine space. For example,
and affine space. For example,
(the Ricci identity);
where 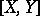 is the commutator of
is the commutator of 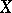 and
and 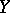 , and
, and
The definition of covariant differentiation remains valid in the more general case when instead of a cross section 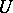 of the tensor bundle with an affine connection one considers a cross section
of the tensor bundle with an affine connection one considers a cross section 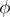 of an arbitrary (real or complex) vector bundle associated with some principal fibre bundle with connection
of an arbitrary (real or complex) vector bundle associated with some principal fibre bundle with connection 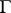 and with a structure group
and with a structure group 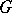 which acts on the fibre by means of a representation in the group of non-singular matrices. There exist definitions of covariant differentiation in the more general situation when the bundle is not necessarily a vector bundle. The common part of these definitions [9] consists in the analytic expression for the parallel displacement of an object or in the condition of being parallel of a cross section which is defined by the requirement that its covariant differential be zero. There are also similar approaches for infinite-dimensional manifolds.
which acts on the fibre by means of a representation in the group of non-singular matrices. There exist definitions of covariant differentiation in the more general situation when the bundle is not necessarily a vector bundle. The common part of these definitions [9] consists in the analytic expression for the parallel displacement of an object or in the condition of being parallel of a cross section which is defined by the requirement that its covariant differential be zero. There are also similar approaches for infinite-dimensional manifolds.
References
| [1] | G. Ricci, T. Levi-Civita, "Méthodes de calcul différentiel absolu et leurs applications" Math. Ann. , 54 (1901) pp. 125–201 |
| [2] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [3] | A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian) |
| [4] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1955) (Translated from French) |
| [5] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
| [6] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) |
| [7] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [8] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) |
| [9] | Ü. Lumiste, "Connection theory in bundle spaces" J. Soviet Math. , 1 (1973) pp. 363–390 Itogi Nauk. Algebra. Topol. Geom. 1969 (1971) pp. 123–168 |
| [10] | R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Deutsch. Verlag Wissenschaft. (1972) |
| [11] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish (1970–1975) pp. 1–5 |
The phrase "covariant differential" is more commonly used for the  tensor field
tensor field 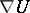 (instead of "covariant derivative" as in the article above); that is,
(instead of "covariant derivative" as in the article above); that is,  and
and 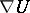 are more or less identified.
are more or less identified.
 -dimensional manifold
-dimensional manifold 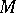 as well as the parallel displacement of vectors and, more generally, tensors, associated with it. Let
as well as the parallel displacement of vectors and, more generally, tensors, associated with it. Let 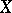 be a smooth vector field,
be a smooth vector field, 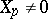 ,
, 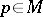 , and let
, and let 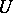 be a tensor field of type
be a tensor field of type 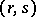 , that is,
, that is,  times contravariant and
times contravariant and  times covariant; by the covariant derivative (with respect to the given connection) of
times covariant; by the covariant derivative (with respect to the given connection) of 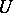 at
at 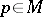 along
along 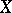 one means the tensor (of the same type
one means the tensor (of the same type 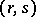 )
)

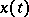 is the point on the integral curve
is the point on the integral curve 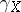 of the vector field
of the vector field 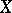 with initial condition
with initial condition 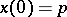 ,
, 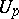 and
and 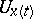 are, respectively, the localizations (values) of
are, respectively, the localizations (values) of 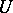 at
at 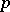 and
and 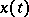 , and
, and 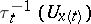 is the result of the parallel displacement of
is the result of the parallel displacement of 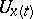 along
along 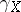 from
from 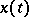 to
to 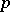 . Thus the basic idea behind the definition of the covariant derivative of a tensor field
. Thus the basic idea behind the definition of the covariant derivative of a tensor field 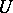 along a vector field
along a vector field 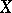 is that, in view of the absence of a natural relation between
is that, in view of the absence of a natural relation between 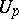 and
and 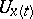 , as they belong to different fibres of the tensor bundle over
, as they belong to different fibres of the tensor bundle over 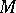 , that is, they are in tensor spaces
, that is, they are in tensor spaces 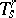 over different tangent spaces
over different tangent spaces 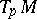 and
and 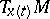 to
to 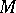 , the difference between
, the difference between 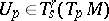 and the image of
and the image of 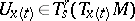 under the parallel displacement along
under the parallel displacement along 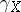 to
to 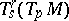 serves as the "increment" of
serves as the "increment" of 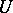 ; one then takes the limit of the ratio of this "increment" to the increment of the argument
; one then takes the limit of the ratio of this "increment" to the increment of the argument 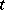 in the usual way. If, in particular, for points
in the usual way. If, in particular, for points 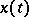 near to
near to 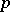 the field
the field 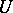 is obtained by parallel displacement of the tensor
is obtained by parallel displacement of the tensor 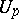 along
along 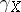 , then
, then 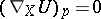 , and therefore, in general, the covariant derivative of
, and therefore, in general, the covariant derivative of 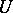 at
at 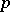 along
along 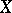 defines the initial rate of the difference of
defines the initial rate of the difference of 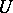 along
along 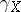 from the result of the parallel displacement of
from the result of the parallel displacement of 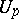 along
along 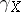 . For tensor fields of zero valency, that is, for functions
. For tensor fields of zero valency, that is, for functions 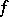 in the ring
in the ring 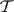 of differentiable functions on
of differentiable functions on 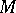 ,
,

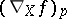 with the derivative of
with the derivative of 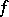 along the vector
along the vector 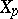 , that is, with
, that is, with 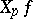 . When
. When 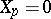 one has, by definition,
one has, by definition, 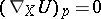 for any tensor field
for any tensor field 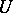 .
.
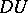 of a tensor field
of a tensor field 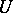 along a smooth curve
along a smooth curve 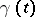 as
as
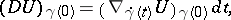
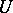 (in the sense described above) under the displacement along
(in the sense described above) under the displacement along 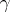 of the point by an infinitesimal segment
of the point by an infinitesimal segment 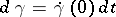 .
.
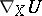 for a tensor field
for a tensor field 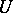 of type
of type 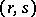 at each point
at each point 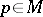 along each vector field
along each vector field 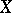 enables one to introduce for
enables one to introduce for 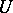 : 1) the covariant differential field
: 1) the covariant differential field 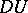 as a tensor
as a tensor 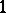 -form with values in the module
-form with values in the module 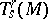 , defined on the vectors of
, defined on the vectors of 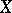 by the formula
by the formula 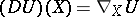 ; 2) the covariant derivative field
; 2) the covariant derivative field 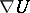 as a tensor field of type
as a tensor field of type 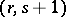 , corresponding canonically to the form
, corresponding canonically to the form 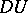 and acting on
and acting on 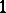 -forms
-forms 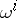 and vectors
and vectors 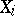 according to the formula
according to the formula
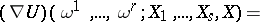
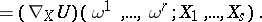
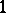 -form
-form 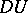 itself but its values at the vectors
itself but its values at the vectors 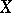 , and in this interpretation
, and in this interpretation 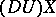 is also converted into a tensor field of type
is also converted into a tensor field of type 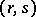 the localization of which, in particular, when
the localization of which, in particular, when 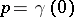 and
and 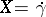 , is the same as the covariant differential
, is the same as the covariant differential 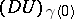 along the curve
along the curve 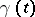 , introduced above. The covariant derivative
, introduced above. The covariant derivative 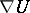 is sometimes called the gradient of the tensor
is sometimes called the gradient of the tensor 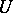 and the derivative, the covariant differential.
and the derivative, the covariant differential.
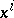 are local coordinates,
are local coordinates, 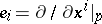 denotes the corresponding basis of the space of vector fields,
denotes the corresponding basis of the space of vector fields, 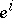 denotes the dual basis for the space of
denotes the dual basis for the space of 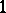 -forms,
-forms, 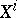 and
and 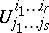 are the coordinates of vector and tensor fields in these bases, and
are the coordinates of vector and tensor fields in these bases, and 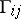 are the coefficients of an affine connection introduced on the manifold
are the coefficients of an affine connection introduced on the manifold 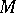 (cf. Linear connection), then, denoting by
(cf. Linear connection), then, denoting by 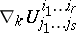 or
or 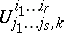 the components of the tensor field
the components of the tensor field 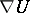 , one obtains the following expressions (as an example,
, one obtains the following expressions (as an example, 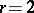 ,
, 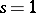 have been chosen):
have been chosen):
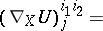

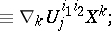
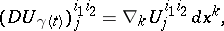
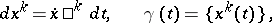
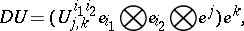
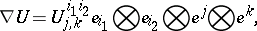
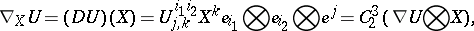
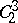 is the operation of contraction (cf. Contraction of a tensor) with respect to the third contravariant and second covariant indices.
is the operation of contraction (cf. Contraction of a tensor) with respect to the third contravariant and second covariant indices.
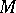 is an affine space and
is an affine space and 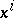 are affine coordinates, then
are affine coordinates, then 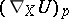 is the ordinary derivative of the tensor field
is the ordinary derivative of the tensor field 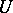 along the vector field
along the vector field 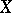 , the
, the 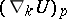 are the partial derivatives of
are the partial derivatives of 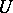 at
at 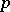 with respect to
with respect to 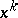 , and
, and 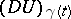 is the ordinary differential of
is the ordinary differential of 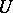 along the curve
along the curve 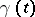 . Thus the covariant derivative emerges as a generalization of ordinary differentiation for which the well-known relationships between the first-order partial derivatives and differentials remain valid.
. Thus the covariant derivative emerges as a generalization of ordinary differentiation for which the well-known relationships between the first-order partial derivatives and differentials remain valid.
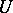 along a curve
along a curve 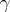 is given by the equation
is given by the equation 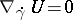 , the equation of a geodesic
, the equation of a geodesic 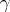 is written in the form
is written in the form 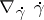 , the integrability condition for a system of equations in covariant derivatives of the first order is reduced to an equation for the alternating difference
, the integrability condition for a system of equations in covariant derivatives of the first order is reduced to an equation for the alternating difference 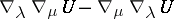 ; exterior differentiation of forms on a manifold and in bundles over it can also be expressed in terms of covariant differentiation; and there are other examples.
; exterior differentiation of forms on a manifold and in bundles over it can also be expressed in terms of covariant differentiation; and there are other examples.
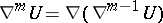 . Generally speaking, the tensor
. Generally speaking, the tensor 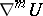 obtained in this way is not symmetric in the last covariant indices; higher covariant derivatives along different vector fields also depend on the order of differentiation. The alternating differences of the covariant derivatives of higher orders are expressed in terms of the curvature tensor
obtained in this way is not symmetric in the last covariant indices; higher covariant derivatives along different vector fields also depend on the order of differentiation. The alternating differences of the covariant derivatives of higher orders are expressed in terms of the curvature tensor 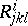 and torsion tensor
and torsion tensor 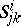 , which together characterize the difference between the manifold
, which together characterize the difference between the manifold 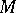 and affine space. For example,
and affine space. For example,
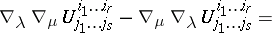
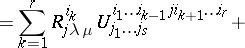
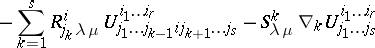
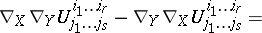
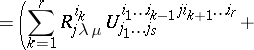
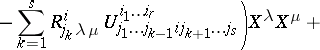
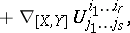
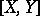 is the commutator of
is the commutator of 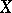 and
and 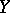 , and
, and
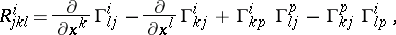
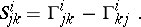
 of the tensor bundle with an affine connection one considers a cross section
of the tensor bundle with an affine connection one considers a cross section  of an arbitrary (real or complex) vector bundle associated with some principal fibre bundle with connection
of an arbitrary (real or complex) vector bundle associated with some principal fibre bundle with connection 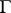 and with a structure group
and with a structure group 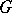 which acts on the fibre by means of a representation in the group of non-singular matrices. There exist definitions of covariant differentiation in the more general situation when the bundle is not necessarily a vector bundle. The common part of these definitions [9] consists in the analytic expression for the parallel displacement of an object or in the condition of being parallel of a cross section which is defined by the requirement that its covariant differential be zero. There are also similar approaches for infinite-dimensional manifolds.
which acts on the fibre by means of a representation in the group of non-singular matrices. There exist definitions of covariant differentiation in the more general situation when the bundle is not necessarily a vector bundle. The common part of these definitions [9] consists in the analytic expression for the parallel displacement of an object or in the condition of being parallel of a cross section which is defined by the requirement that its covariant differential be zero. There are also similar approaches for infinite-dimensional manifolds.
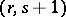 tensor field
tensor field 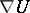 (instead of "covariant derivative" as in the article above); that is,
(instead of "covariant derivative" as in the article above); that is,  and
and 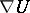 are more or less identified.
are more or less identified.