Covariant derivative
A generalization of the notion of a derivative to fields of different geometrical objects on manifolds, such as vectors, tensors, forms, etc. It is a linear operator  acting on the module of tensor fields
acting on the module of tensor fields  of given valency and defined with respect to a vector field
of given valency and defined with respect to a vector field  on a manifold
on a manifold  and satisfying the following properties:
and satisfying the following properties:
1)  ,
,
2)  , where
, where  and
and  are differentiable functions on
are differentiable functions on 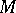 . This mapping is trivially extended by linearity to the algebra of tensor fields and one additionally requires for the action on tensors
. This mapping is trivially extended by linearity to the algebra of tensor fields and one additionally requires for the action on tensors  of different valency:
of different valency:
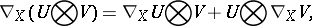 |
where 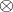 denotes the tensor product. Thus
denotes the tensor product. Thus 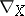 is a derivation on the algebra of tensor fields (cf. Derivation in a ring); it has the additional properties of commuting with operations of contraction (cf. Contraction of a tensor), skew-symmetrization (cf. Alternation) and symmetrization of tensors (cf. Symmetrization (of tensors)).
is a derivation on the algebra of tensor fields (cf. Derivation in a ring); it has the additional properties of commuting with operations of contraction (cf. Contraction of a tensor), skew-symmetrization (cf. Alternation) and symmetrization of tensors (cf. Symmetrization (of tensors)).
Properties 1) and 2) of 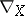 (for vector fields) allow one to introduce on
(for vector fields) allow one to introduce on  a linear connection (and the corresponding parallel displacement) and on the basis of this, to give a local definition of a covariant derivative which, when extended to the whole manifold, coincides with the operator
a linear connection (and the corresponding parallel displacement) and on the basis of this, to give a local definition of a covariant derivative which, when extended to the whole manifold, coincides with the operator  defined above; see also Covariant differentiation.
defined above; see also Covariant differentiation.
Comments
There is not much of a difference between the notions of a covariant derivative and covariant differentiation and both are used in the same context.
Covariant derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant_derivative&oldid=18018