Covariance
A numerical characteristic of the joint distribution of two random variables, equal to the mathematical expectation of the product of the deviations of these two random variables from their mathematical expectations. The covariance is defined for random variables  and
and  with finite variance and is usually denoted by
with finite variance and is usually denoted by  . Thus,
. Thus,
 |
so that  ;
;  . The covariance naturally occurs in the expression for the variance of the sum of two random variables:
. The covariance naturally occurs in the expression for the variance of the sum of two random variables:
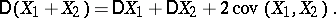 |
If  and
and  are independent random variables, then
are independent random variables, then 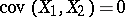 . The covariance gives a characterization of the dependence of the random variables; the correlation coefficient is defined by means of the covariance. In order to statistically estimate the covariance one uses the sample covariance, computed from the formula
. The covariance gives a characterization of the dependence of the random variables; the correlation coefficient is defined by means of the covariance. In order to statistically estimate the covariance one uses the sample covariance, computed from the formula
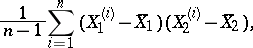 |
where the 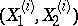 ,
, 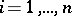 , are independent random variables and
, are independent random variables and 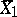 and
and 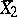 are their arithmetic means.
are their arithmetic means.
Comments
In the Western literature one always uses 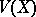 or
or 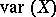 for the variance, instead of
for the variance, instead of 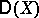 .
.
Covariance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariance&oldid=11255