Cousin problems

Problems named after P. Cousin [1], who first solved them for certain simple domains in the complex -dimensional space .

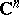First (additive) Cousin problem.

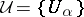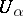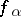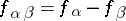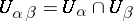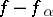Let be a covering of a complex manifold by open subsets , in each of which is defined a meromorphic function ; assume that the functions are holomorphic in for all (compatibility condition). It is required to construct a function which is meromorphic on the entire manifold and is such that the functions are holomorphic in for all . In other words, the problem is to construct a global meromorphic function with locally specified polar singularities.

The functions 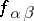, defined in the pairwise intersections 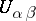of elements of 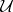, define a holomorphic 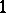-cocycle for 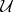, i.e. they satisfy the conditions

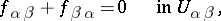(1)

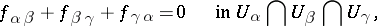for all 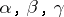. A more general problem (known as the first Cousin problem in cohomological formulation) is the following. Given holomorphic functions 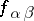in the intersections 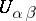, satisfying the cocycle conditions (1), it is required to find functions 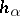, holomorphic in 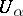, such that

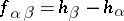(2)

for all 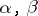. If the functions 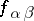correspond to the data of the first Cousin problem and the above functions 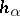exist, then the function

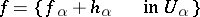is defined and meromorphic throughout 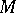and is a solution of the first Cousin problem. Conversely, if 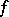is a solution of the first Cousin problem with data 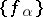, then the holomorphic functions 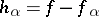satisfy (2). Thus, a specific first Cousin problem is solvable if and only if the corresponding cocycle is a holomorphic coboundary (i.e. satisfies condition (2)).

The first Cousin problem may also be formulated in a local version. To each set of data 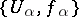satisfying the compatibility condition there corresponds a uniquely defined global section of the sheaf 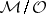, where 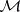and 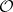are the sheaves of germs of meromorphic and holomorphic functions, respectively; the correspondence is such that any global section of 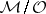corresponds to some first Cousin problem (the value of the section 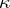corresponding to data 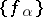at a point 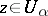is the element of 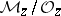with representative 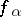). The mapping of global sections 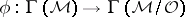maps each meromorphic functi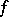on on 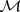to a section 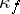of 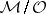, where 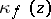is the class in 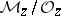of the germ of 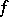at the point , 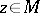. The localized first Cousin problem is then: Given a global section 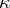of the sheaf 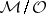, to find a meromorphic functi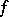on on 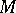(i.e. a section of 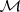) such that .

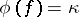Theorems concerning the solvability of the first Cousin problem may be regarded as a multi-dimensional generalization of the Mittag-Leffler theorem on the construction of a meromorphic function with prescribed poles. The problem in cohomological formulation, with a fixed covering 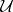, is solvable (for arbitrary compatible 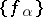) if and only if 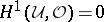(the Čech cohomology for 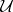with holomorphic coefficients is trivial).

A specific first Cousin problem on 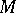is solvable if and only if the corresponding section of 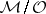belongs to the image of the mapping 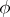. An arbitrary first Cousin problem on 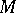is solvable if and only if 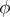is surjective. On any complex manifold 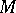one has an exact sequence

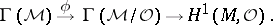If the Čech cohomology for 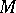with coefficients in 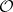is trivial (i.e. 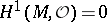), then 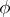is surjective and 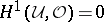for any covering 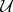of 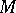. Thus, if , any first Cousin problem is solvable on 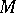(in the classical, cohomological and local version). In particular, the problem is solvable in all domains of holomorphy and on Stein manifolds (cf. Stein manifold). If , then the first Cousin problem in 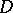is solvable if and only if 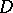is a domain of holomorphy. An example of an unsolvable first Cousin problem is: , , , , .

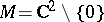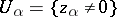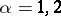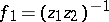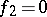Second (multiplicative) Cousin problem.

Given an open covering 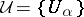of a complex manifold and, in each , a meromorphic function 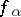, 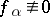on each component of 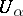, with the assumption that the functions 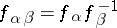are holomorphic and nowhere vanishing in 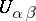for all 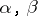(compatibility condition). It is required to construct a meromorphic functi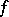on on 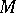such that the functions 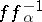are holomorphic and nowhere vanishing in 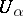for all .

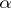The cohomological formulation of the second Cousin problem is as follows. Given the covering 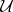and functions , holomorphic and nowhere vanishing in the intersections 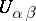, and forming a multiplicative 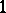-cocycle, i.e.

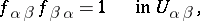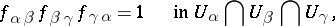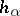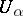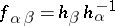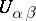it is required to find functions , holomorphic and nowhere vanishing in , such that in for all 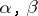. If the cocycle 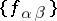corresponds to the data of a second Cousin problem and the required 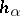exist, then the function 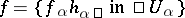is defined and meromorphic throughout 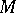and is a solution to the given second Cousin problem. Conversely, if a specific second Cousin problem is solvable, then the corresponding cocycle is a holomorphic coboundary.

The localized second Cousin problem. To each set of data 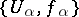for the second Cousin problem there corresponds a uniquely defined global section of the sheaf 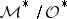(in analogy to the first Cousin problem), where 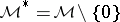(with 0 the null section) is the multiplicative sheaf of germs of meromorphic functions and 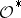is the subsheaf of 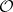in which each stalk 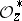consists of germs of holomorphic functions that do not vanish at . The mapping of global sections

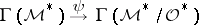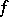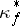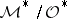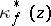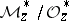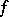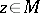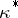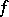maps a meromorphic function to a section of the sheaf , where is the class in of the germ of at , . The localized second Cousin problem is: Given a global section of the sheaf , to find a meromorphic function on 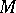, 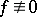on the components of 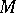(i.e. a global section of 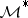), such that .

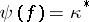The sections of 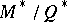uniquely correspond to divisors (cf. Divisor), therefore 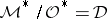is called the sheaf of germs of divisors. A divisor on a complex manifold 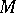is a formal locally finite sum 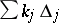, where 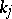are integers and 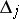analytic subsets of 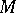of pure codimension 1. To each meromorphic function 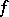corresponds the divisor whose terms are the irreducible components of the zero and polar sets of 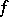with respective multiplicities 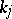, with multiplicities of zeros considered positive and those of poles negative. 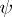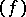The mapping maps each function to its divisor ; such divisors are called proper divisors. The second Cousin problem in terms of divisors is: Given a divisor 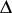on the manifold 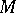, to construct a meromorphic functi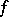on on 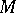such that .

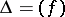Theorems concerning the solvability of the second Cousin problem may be regarded as multi-dimensional generalizations of Weierstrass' theorem on the construction of a meromorphic function with prescribed zeros and poles. As in the case of the first Cousin problem, a necessary and sufficient condition for the solvability of any second Cousin problem in cohomological version is that 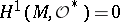. Unfortunately, the sheaf 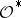is not coherent, and this condition is less effective. The attempt to reduce a given second Cousin problem to a first Cousin problem by taking logarithms encounters an obstruction in the form of an integral -cocycle, and one obtains an exact sequence

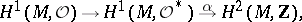where 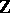is the constant sheaf of integers. Thus, if 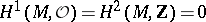, any second Cousin problem is solvable on 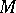, and any divisor is proper. If 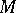is a Stein manifold, then 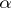is an isomorphism; hence the topological condition 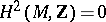on a Stein manifold 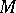is necessary and sufficient for the second Cousin problem in cohomological version to be solvable. The composite mapping ,

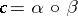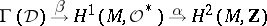maps each divisor 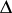to an element 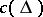of the group 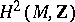, which is known as the Chern class of 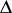. The specific second Cousin problem corresponding to is solvable, assuming 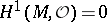, if and only if the Chern class of 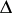is trivial: 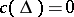. On a Stein manifold, the mapping is surjective; moreover, every element in 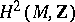may be expressed as 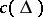for some divisor 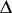with positive multiplicities 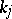. Thus, the obstructions to the solution of the second Cousin problem on a Stein manifold 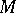are completely described by the group .

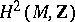Examples.

1) 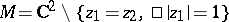; the first Cousin problem is unsolvable; the second Cousin problem is unsolvable, e.g., for the divisor 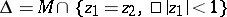with multiplicity 1.

2) 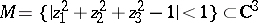, is one of the components of the intersection of 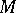and the plane 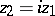with multiplicity 1. The second Cousin problem is unsolvable ( 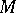is a domain of holomorphy, the first Cousin problem is solvable).

3) The first and second Cousin problems are solvable in domains 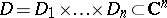, where 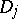are plane domains and all 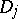, with the possible exception of one, are simply connected.

References

[1]	P. Cousin, "Sur les fonctions de variables" Acta Math. , 19 (1895) pp. 1–62
[2]	B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian)
[3]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)

Comments

The Cousin problems are related to the Poincaré problem (is a meromorphic function given on a complex manifold 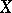globally the quotient of two holomorphic functions whose germs are relatively prime for all 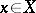?) and to the, more algebraic, Theorems A and B of H. Cartan and J.-P. Serre, cf. [a1], [a2], [a3].

References

[a1]	C.A. Cazacu, "Theorie der Funktionen mehreren komplexer Veränderlicher" , Birkhäuser (1975) (Translated from Rumanian)
[a2]	H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German)
[a3]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Sect. 4.5
[a4]	S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Chapt. 6
[a5]	R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 6