Cosine
One of the trigonometric functions:
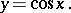 |
Its domain of definition is the entire real line; its range of values is the closed interval 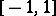 ; the cosine is an even periodic function (with period
; the cosine is an even periodic function (with period 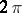 ). The cosine and the sine are related via the formula
). The cosine and the sine are related via the formula
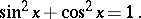 |
The cosine and the secant are related via the formula
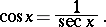 |
The derivative of the cosine is:
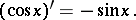 |
The integral of the cosine is:
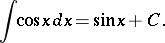 |
The series expansion is:
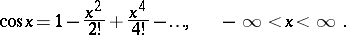 |
The inverse function is the arccosine.
The cosine and sine of a complex argument  are related to the exponential function by Euler's formula:
are related to the exponential function by Euler's formula:
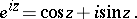 |
If  is a real number, then
is a real number, then
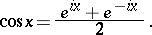 |
If  (a purely imaginary number), then
(a purely imaginary number), then
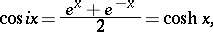 |
where 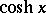 is the hyperbolic cosine.
is the hyperbolic cosine.
Comments
A geometric interpretation of the cosine of an argument (angle) 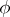 is as follows. Consider the unit circle
is as follows. Consider the unit circle 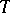 in the (complex) plane with origin
in the (complex) plane with origin  . Let
. Let 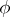 denote the angle between the radius (thought of as varying) and the positive
denote the angle between the radius (thought of as varying) and the positive  -axis. Then
-axis. Then 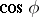 is equal to the (signed) distance from the point
is equal to the (signed) distance from the point 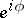 on
on 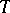 corresponding to
corresponding to 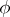 to the
to the  -axis. See also Sine.
-axis. See also Sine.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Cosine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cosine&oldid=14514