Correlation property for sequences
Complex-valued  -periodic sequences (i.e. sequences
-periodic sequences (i.e. sequences  with
with 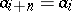 ,
, 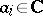 ) with "good" correlation properties have many applications in signal processing (spread spectrum and code division multiple access communication systems, see [a10]). A good survey is [a9]. Periodic sequences are recurring or shift register sequences, see [a2].
) with "good" correlation properties have many applications in signal processing (spread spectrum and code division multiple access communication systems, see [a10]). A good survey is [a9]. Periodic sequences are recurring or shift register sequences, see [a2].
If  and
and 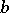 are
are  -periodic sequences, one defines
-periodic sequences, one defines 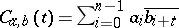 . These numbers are called the periodic correlation coefficients (in case
. These numbers are called the periodic correlation coefficients (in case 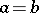 , periodic autocorrelation coefficients). Sometimes also the aperiodic correlation
, periodic autocorrelation coefficients). Sometimes also the aperiodic correlation  is of interest. The odd correlation of
is of interest. The odd correlation of 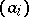 and
and 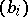 is
is 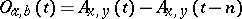 ,
, 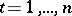 .
.
The goal is the design of large sets 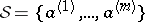 of
of  -periodic sequences such that
-periodic sequences such that
 |
 |
(or the respective value for the aperiodic correlation) is small. Sequences with  ,
,  , are called perfect. Perfect sequences whose entries are
, are called perfect. Perfect sequences whose entries are 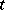 th roots of unity (
th roots of unity (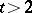 ) are known for many periods
) are known for many periods  , but no example of a
, but no example of a 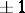 -sequence with period
-sequence with period 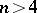 is known (the perfect sequence conjecture: there are no perfect binary sequences with
is known (the perfect sequence conjecture: there are no perfect binary sequences with 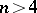 ). In the aperiodic case, the
). In the aperiodic case, the 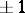 -sequences with odd period
-sequences with odd period  and aperiodic correlation coefficients
and aperiodic correlation coefficients  and
and 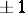 (Barker sequences) have been classified [a12]. If
(Barker sequences) have been classified [a12]. If  is even, the existence of an
is even, the existence of an  -periodic Barker sequence implies the existence of an
-periodic Barker sequence implies the existence of an  -periodic perfect
-periodic perfect 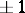 -sequence.
-sequence.
If one assumes that the sequences are normalized, i.e. 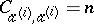 , then it is known that for
, then it is known that for 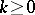 ,
,
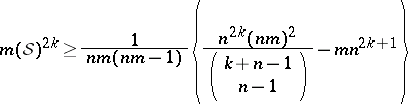 |
and, if the entries of the sequences are just 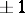 :
:
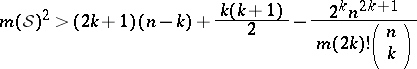 |
for 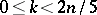 . If the entries of the sequences are
. If the entries of the sequences are  th roots of unity (
th roots of unity (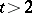 ), then the bound is
), then the bound is
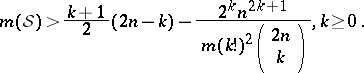 |
The first bound is due to L.R. Welch, the second two bounds are due to V.M. Sidel'nikov. In all cases, 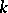 is an integer. Some improvements of these bounds are known. Similar bounds hold for the maximum odd correlation coefficient [a7].
is an integer. Some improvements of these bounds are known. Similar bounds hold for the maximum odd correlation coefficient [a7].
Important classes of sequences are derived from so-called 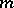 -sequences
-sequences  , where
, where 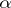 is a primitive element of the finite field
is a primitive element of the finite field 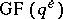 and
and  . The sequence
. The sequence 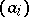 is defined over a finite field. The complex-valued sequences corresponding to such finite field sequences are
is defined over a finite field. The complex-valued sequences corresponding to such finite field sequences are  , where
, where 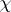 is a homomorphism from the additive group of the field into the multiplicative group of
is a homomorphism from the additive group of the field into the multiplicative group of 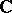 . The
. The 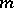 -sequences yield complex sequences with autocorrelation coefficients
-sequences yield complex sequences with autocorrelation coefficients 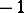 . The
. The  -decimation of an
-decimation of an  -periodic sequence is
-periodic sequence is 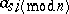 . Systematic investigations of the correlation properties between
. Systematic investigations of the correlation properties between 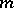 -sequences and their decimations can be found in [a4] and [a11]. The
-sequences and their decimations can be found in [a4] and [a11]. The 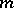 -sequences are recurring sequences of maximum period length. Their good autocorrelation properties show that they have good "random" properties (pseudo-noise sequences).
-sequences are recurring sequences of maximum period length. Their good autocorrelation properties show that they have good "random" properties (pseudo-noise sequences).
In many cases, variations of the construction of 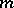 -sequences yield sets of sequences with optimal correlation properties with respect to the Welch and Sidel'nikov bounds: The cases
-sequences yield sets of sequences with optimal correlation properties with respect to the Welch and Sidel'nikov bounds: The cases 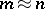 and
and 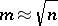 have been investigated intensively. Regarding binary sequences, both the Gold sequences (
have been investigated intensively. Regarding binary sequences, both the Gold sequences (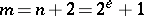 ) and the Kasami sequences (
) and the Kasami sequences (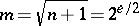 ) are asymptotically optimal. (One says that a family
) are asymptotically optimal. (One says that a family 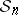 of sets of
of sets of  -periodic sequences is asymptotically optimal if
-periodic sequences is asymptotically optimal if 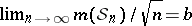 , is best possible. If
, is best possible. If  , the lower bounds show that
, the lower bounds show that 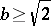 for binary and
for binary and  for arbitrary complex valued sequences. For
for arbitrary complex valued sequences. For 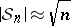 , one has
, one has  .) Sequences whose entries are
.) Sequences whose entries are 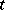 th roots of unity (
th roots of unity ( ) and which are optimal have been constructed (
) and which are optimal have been constructed (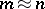 ,
,  prime [a5];
prime [a5];  ,
,  [a1]). The latter construction is of particular interest in view of its connection with Kerdock and Preparata codes (cf. Kerdock and Preparata codes) and their linearity as codes over
[a1]). The latter construction is of particular interest in view of its connection with Kerdock and Preparata codes (cf. Kerdock and Preparata codes) and their linearity as codes over 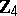 , see [a3]. More sequences with good correlation properties where
, see [a3]. More sequences with good correlation properties where  is not a prime number can be constructed. In these constructions, sequences over Galois rings instead of finite fields are converted via homomorphisms
is not a prime number can be constructed. In these constructions, sequences over Galois rings instead of finite fields are converted via homomorphisms 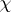 into complex-valued sequences. A systematic investigation of shift register sequences over rings can be found in [a6].
into complex-valued sequences. A systematic investigation of shift register sequences over rings can be found in [a6].
Other important classes of sequences with good correlation properties are bent function sequences, [a8].
References
| [a1] | S. Boztas, A.R. Hammons, P.V. Kumar, "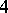 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | S.W. Golomb, "Shift register sequences" , Aegean Park, Laguna Hills (California) (1982) (Edition: Revised) |
| [a3] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 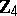 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a4] | T. Helleseth, "Some results about the cross-correlation function between two maximal linear sequences" Discrete Math. , 16 (1976) pp. 209–232 |
| [a5] | P.V. Kumar, O. Moreno, "Prime-phase sequences with periodic correlation properties better than binary sequences" IEEE Trans. Information Th. , 37 (1991) pp. 603–616 |
| [a6] | V.L. Kurakin, A.S. Kuzmin, A.V. Mikhalev, A.A. Nechaev, "Linear recurring sequences over rings and modules" J. Math. Sci. , 76 (1995) pp. 2793–2915 |
| [a7] | W.H. Mow, "On the bounds on odd correlation of sequences" IEEE Trans. Information Th. , 40 (1994) pp. 954–955 |
| [a8] | J.D. Olsen, R.A. Scholtz, L.R. Welch, "Bent-function sequences" IEEE Trans. Information Th. , 28 (1982) pp. 858–864 |
| [a9] | D.V. Sarwate, M.B. Pursley, "Crosscorrelation properties of pseudorandom and related sequences" Proc. IEEE , 68 (1980) pp. 593–619 |
| [a10] | M. Simon, J. Omura, R. Scholtz, B. Levitt, "Spread Spectrum Communications" , I , Computer Sci. Press (1985) |
| [a11] | H.M. Trachtenberg, "On the cross-correlation functions of maximal recurring sequences" Ph.D. Thesis, Univ. Southern California (1970) |
| [a12] | R. Turyn, J. Storer, "On binary sequences" Proc. Amer. Math. Soc. , 12 (1961) pp. 394–399 |
Correlation property for sequences. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation_property_for_sequences&oldid=13199