Correlation coefficient

A numerical characteristic of the joint distribution of two random variables, expressing a relationship between them. The correlation coefficient for random variables and with mathematical expectations and and non-zero variances and is defined by

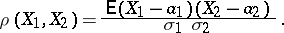The correlation coefficient of and 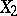is simply the covariance of the normalized variables and 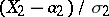. The correlation coefficient is symmetric with respect to 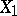and 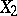and is invariant under change of the origin and scaling. In all cases . The importance of the correlation coefficient as one of the possible measures of dependence is determined by its following properties: 1) if 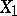and 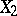are independent, then (the converse is not necessarily true). Random variables for which 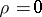are said to be non-correlated. 2) if and only if the dependence between the random variables is linear:

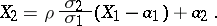The difficulty of interpreting 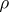as a measure of dependence is that the equality may be valid for both independent and dependent random variables; in the general case, a necessary and sufficient condition for independence is that the maximal correlation coefficient equals zero. Thus, the correlation coefficient does not exhaust all types of dependence between random variables and it is a measure of linear dependence only. The degree of this linear dependence is characterized as follows: The random variable

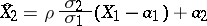gives a linear representation of in terms of 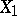which is best in the sense that

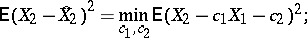see also Regression. As characteristic correlations between several random variables there are the partial correlation coefficient and the multiple-correlation coefficient. For methods for testing independence hypotheses and using correlation coefficients to study correlation, see Correlation (in statistics).