Difference between revisions of "Cornish-Fisher expansion"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Cornish–Fisher expansion to Cornish-Fisher expansion: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
An asymptotic expansion of the quantiles of a distribution (close to the normal standard one) in terms of the corresponding quantiles of the standard normal distribution, in powers of a small parameter. It was studied by E.A. Cornish and R.A. Fisher [1]. If 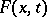 is a distribution function depending on
is a distribution function depending on 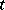 as a parameter, if
as a parameter, if 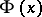 is the normal distribution function with parameters
is the normal distribution function with parameters 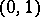 , and if
, and if 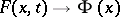 as
as 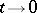 , then, subject to certain assumptions on
, then, subject to certain assumptions on 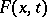 , the Cornish–Fisher expansion of the function
, the Cornish–Fisher expansion of the function 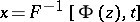 (where
(where 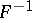 is the function inverse to
is the function inverse to 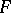 ) has the form
) has the form
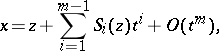 | (1) |
where the 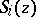 are certain polynomials in
are certain polynomials in  . Similarly, one defines the Cornish–Fisher expansion of the function
. Similarly, one defines the Cornish–Fisher expansion of the function 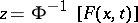 (
(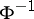 being the function inverse to
being the function inverse to 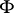 ) in powers of
) in powers of  :
:
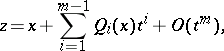 | (2) |
where the 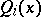 are certain polynomials in
are certain polynomials in  . Formula (2) is obtained by expanding
. Formula (2) is obtained by expanding 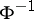 in a Taylor series about the point
in a Taylor series about the point 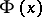 and using the Edgeworth expansion. Formula (1) is the inversion of (2).
and using the Edgeworth expansion. Formula (1) is the inversion of (2).
If 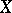 is a random variable with distribution function
is a random variable with distribution function 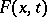 , then the variable
, then the variable 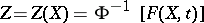 is normally distributed with parameters
is normally distributed with parameters 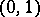 , and, as follows from (2),
, and, as follows from (2), 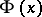 approximates the distribution function of the variable
approximates the distribution function of the variable
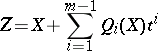 |
as 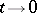 better than it approximates
better than it approximates 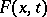 . If
. If 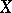 has zero expectation and unit variance, then the first terms of the expansion (1) have the form
has zero expectation and unit variance, then the first terms of the expansion (1) have the form
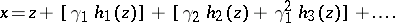 |
Here 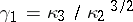 ,
, 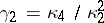 , with
, with 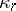 the
the  -th cumulant of
-th cumulant of 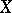 ,
, 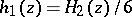 ,
, 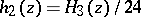 ,
, 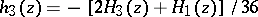 , and with
, and with 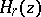 the Hermite polynomials, defined by the relation
the Hermite polynomials, defined by the relation
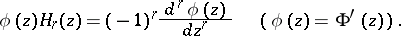 |
Concerning expansions for random variables obeying limit laws from the family of Pearson distributions see [3]. See also Random variables, transformations of.
References
| [1] | E.A. Cornish, R.A. Fisher, "Moments and cumulants in the specification of distributions" Rev. Inst. Internat. Statist. , 5 (1937) pp. 307–320 |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , 3. Design and analysis , Griffin (1969) |
| [3] | L.N. Bol'shev, "Asymptotically Pearson transformations" Theor. Probab. Appl. , 8 (1963) pp. 121–146 Teor. Veroyatnost. i Primenen. , 8 : 2 (1963) pp. 129–155 |
Comments
For the methods of using an Edgeworth expansion to obtain (2) (see also Edgeworth series), see also [a1].
References
| [a1] | P.J. Bickel, "Edgeworth expansions in non parametric statistics" Ann. Statist. , 2 (1974) pp. 1–20 |
| [a2] | N.L. Johnson, S. Kotz, "Distributions in statistics" , 1 , Houghton Mifflin (1970) |
Cornish-Fisher expansion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cornish-Fisher_expansion&oldid=14424