Core of a subgroup
From Encyclopedia of Mathematics
Let  be a subgroup of
be a subgroup of 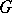 . The core of
. The core of  is the maximal subgroup of
is the maximal subgroup of 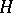 that is normal in
that is normal in  (cf. also Normal subgroup). It follows that
(cf. also Normal subgroup). It follows that
 |
If the index 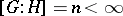 , then
, then  divides
divides  .
.
Let  and define the permutation representation of
and define the permutation representation of 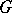 on the set of right cosets of
on the set of right cosets of 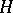 in
in  . Then its kernel is the core of
. Then its kernel is the core of  in
in  .
.
References
| [a1] | M. Suzuki, "Group theory" , I , Springer (1982) |
| [a2] | W.R. Scott, "Group theory" , Dover, reprint (1987) (Original: Prentice-Hall, 1964) |
How to Cite This Entry:
Core of a subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Core_of_a_subgroup&oldid=16708
Core of a subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Core_of_a_subgroup&oldid=16708
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article