Coproduct
of a family of objects in a category
A concept describing the (categorical analogues of the) construction of a direct sum of modules or a discrete union (bouquet) of sets in the language of morphisms. Let 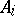 ,
, 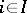 , be an indexed family of objects in a category
, be an indexed family of objects in a category 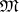 . An object
. An object 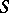 , together with morphisms
, together with morphisms 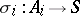 , is called the coproduct of the family
, is called the coproduct of the family 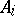 ,
, 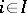 , if for any family of morphisms
, if for any family of morphisms 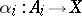 ,
, 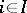 , there exists a unique morphism
, there exists a unique morphism 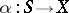 such that
such that 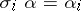 ,
, 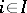 . The morphisms
. The morphisms 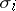 are called the imbeddings of the coproduct; the coproduct is denoted by
are called the imbeddings of the coproduct; the coproduct is denoted by 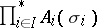 ,
, 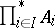 , or
, or 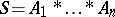 in case
in case 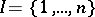 . The morphism
. The morphism 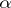 figuring in the definition of the coproduct is sometimes denoted by
figuring in the definition of the coproduct is sometimes denoted by 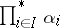 or
or 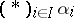 . The coproduct of a family of objects is defined uniquely up to an isomorphism; it is associative and commutative. The coproduct is the dual concept of the product of a family of objects in a category.
. The coproduct of a family of objects is defined uniquely up to an isomorphism; it is associative and commutative. The coproduct is the dual concept of the product of a family of objects in a category.
The coproduct of the empty family of objects is the left zero (initial object) of the category. In an Abelian category, the coproduct is frequently called the direct sum of the family  ,
, 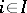 , and is denoted by
, and is denoted by 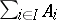 , or
, or 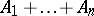 in case
in case 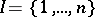 . In most categories of structured sets, the coproduct of a family of objects coincides with the free product of the family, and as a rule requires special description. Thus, in the category of groups, the coproduct is the free product of groups; in the category of modules it is the direct sum of modules; etc.
. In most categories of structured sets, the coproduct of a family of objects coincides with the free product of the family, and as a rule requires special description. Thus, in the category of groups, the coproduct is the free product of groups; in the category of modules it is the direct sum of modules; etc.
In a category with null morphisms, if 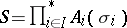 is a coproduct, there exist uniquely defined morphisms
is a coproduct, there exist uniquely defined morphisms 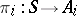 such that
such that 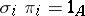 ,
, 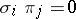 . In an Abelian category the coproduct and the product of a finite family of objects are one and the same.
. In an Abelian category the coproduct and the product of a finite family of objects are one and the same.
References
| [1] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
Comments
Also in not necessarily Abelian categories the coproduct of a family of objects is frequently called the sum of a family of objects or the direct sum of a family of objects. Often used notations are 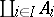 ,
, 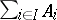 and
and 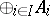 .
.
References
| [a1] | N. Popescu, "Abelian categories with applications to rings and modules" , Acad. Press (1973) |
| [a2] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
Coproduct. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coproduct&oldid=14177