Convexity, logarithmic
From Encyclopedia of Mathematics
The property of a non-negative function 
, defined on some interval, that can be described as follows: If for any 
and 
in this interval and for any 
, 
with 
the inequality
 |
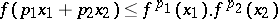is satisfied, 
is called logarithmically convex. If a function is logarithmically convex, it is either identically equal to zero or is strictly positive and 
is a convex function (of a real variable).
How to Cite This Entry:
Convexity, logarithmic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convexity,_logarithmic&oldid=11737
Convexity, logarithmic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convexity,_logarithmic&oldid=11737
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article