Convex hull

of a set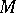

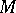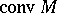The minimal convex set containing ; it is the intersection of all convex sets containing . The convex hull of a set is denoted by . In the Euclidean space 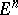the convex hull is the set of possible locations of the centre of gravity of a mass which can be distributed in 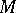in different manners. Each point of the convex hull is the centre of gravity of a mass concentrated at not more than 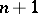points (Carathéodory's theorem).

The closure of the convex hull is called the closed convex hull. It is the intersection of all closed half-spaces containing 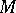or is identical with 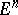. The part of the boundary of the convex hull not adjacent to 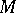has the local structure of a developable hypersurface. In 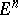the convex hull of a bounded closed set 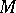is the convex hull of the extreme points of 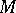(an extreme point of is a point of this set which is not an interior point of any segment belonging to ).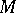

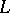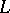In addition to Euclidean spaces, convex hulls are usually considered in locally convex linear topological spaces . In , the convex hull of a compact set 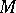is the closed convex hull of its extreme points (the Krein–Mil'man theorem).

References

[1]	R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)
[2]	R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966)