Contragredient representation
to a representation 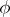 of a group
of a group 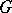 in a linear space
in a linear space 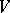
The representation 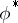 of the same group
of the same group 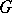 in the dual space
in the dual space 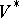 of
of 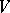 defined by the rule
defined by the rule
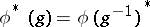 |
for all 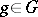 , where
, where  denotes taking adjoints.
denotes taking adjoints.
More generally, if 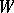 is a linear space over the same field
is a linear space over the same field 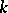 as
as 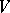 and
and 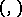 is a non-degenerate bilinear form (pairing) on
is a non-degenerate bilinear form (pairing) on 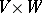 with values in
with values in 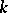 , then a representation
, then a representation 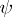 of
of 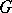 in
in 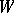 is called the representation contragredient to
is called the representation contragredient to 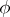 with respect to the form
with respect to the form 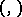 if
if
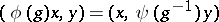 |
for all 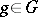 ,
, 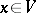 ,
, 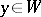 .
.
For example, if 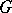 is the general linear group of a finite-dimensional space
is the general linear group of a finite-dimensional space 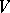 , then the natural representation of
, then the natural representation of 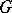 in the space of covariant tensors of fixed rank on
in the space of covariant tensors of fixed rank on 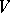 is the representation contragredient to the natural representation of
is the representation contragredient to the natural representation of 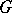 in the space of contravariant tensors of the same rank on
in the space of contravariant tensors of the same rank on 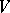 .
.
Let 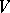 be finite-dimensional over
be finite-dimensional over 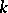 , let
, let 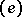 be a basis of it, and let
be a basis of it, and let 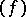 be the basis dual to
be the basis dual to 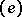 in
in 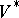 . Then, for any
. Then, for any 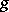 in
in 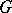 , the matrix of
, the matrix of  in the basis
in the basis 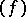 is obtained from the matrix of the operator
is obtained from the matrix of the operator  in the basis
in the basis 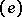 by taking the transpose of the inverse. If
by taking the transpose of the inverse. If 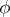 is irreducible, then so is
is irreducible, then so is 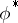 . If
. If 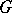 is a Lie group with Lie algebra
is a Lie group with Lie algebra 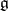 , and
, and 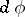 and
and 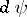 are the representations of the algebra
are the representations of the algebra 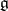 induced, respectively, by two representations
induced, respectively, by two representations 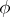 and
and 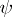 of
of 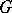 in spaces
in spaces 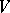 and
and 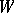 that are contragredient with respect to the pairing
that are contragredient with respect to the pairing 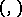 , then
, then
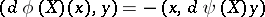 | (*) |
for all 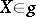 ,
, 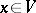 ,
, 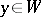 . Representations of a Lie algebra
. Representations of a Lie algebra 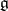 satisfying the condition (*) are also called contragredient representations with respect to
satisfying the condition (*) are also called contragredient representations with respect to 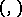 .
.
Suppose further that 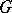 is a complex, connected, simply-connected semi-simple Lie group and that
is a complex, connected, simply-connected semi-simple Lie group and that 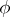 is an irreducible finite-dimensional representation of it in a linear space
is an irreducible finite-dimensional representation of it in a linear space 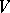 . The weights of the representation
. The weights of the representation 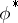 are opposite to those of
are opposite to those of 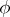 (see Weight of a representation of a Lie algebra), the lowest weight of
(see Weight of a representation of a Lie algebra), the lowest weight of 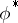 being opposite to the highest weight of
being opposite to the highest weight of 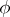 (see Cartan theorem on the highest (weight) vector). The representations
(see Cartan theorem on the highest (weight) vector). The representations 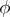 and
and 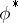 are equivalent if and only if there is a non-zero bilinear form on
are equivalent if and only if there is a non-zero bilinear form on 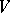 that is invariant with respect to
that is invariant with respect to 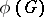 . If such a form exists, then it is non-degenerate and either symmetric or skew-symmetric. The set of numerical marks of the highest weight of the representation
. If such a form exists, then it is non-degenerate and either symmetric or skew-symmetric. The set of numerical marks of the highest weight of the representation 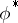 is obtained from the set of numerical marks of
is obtained from the set of numerical marks of 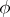 by applying the substitution induced by the following automorphism
by applying the substitution induced by the following automorphism  of the Dynkin diagram of simple roots
of the Dynkin diagram of simple roots 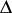 of
of 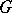 :
:
a)  takes each connected component
takes each connected component 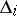 ,
,  , of
, of 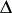 into itself;
into itself;
b) if 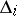 is a diagram of type
is a diagram of type 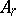 ,
, 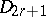 or
or 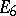 , then the restriction of
, then the restriction of  to
to 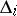 is uniquely defined as the unique element of order 2 in the automorphism group of
is uniquely defined as the unique element of order 2 in the automorphism group of 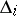 ; in the remaining cases the restriction of
; in the remaining cases the restriction of  to
to 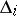 is the identity.
is the identity.
References
| [1] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) MR0793377 Zbl 0484.22018 |
| [2] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) MR0412321 Zbl 0342.22001 |
| [3] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
| [4] | E.B. Vinberg, A.L. Onishchik, "Seminar on algebraic groups and Lie groups 1967/68" , Springer (Forthcoming) (Translated from Russian) |
Comments
If 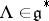 is the highest weight of the highest weight representation
is the highest weight of the highest weight representation 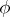 , then the set of numerical marks of
, then the set of numerical marks of 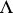 is simply the ordered set of integers
is simply the ordered set of integers 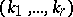 ,
, 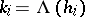 ; cf. Cartan theorem, especially when written as labels at the corresponding nodes of the Dynkin diagram.
; cf. Cartan theorem, especially when written as labels at the corresponding nodes of the Dynkin diagram.
Contragredient representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contragredient_representation&oldid=13402