Contraction semi-group
A one-parameter strongly-continuous semi-group  ,
,  ,
,  , of linear operators in a Banach space
, of linear operators in a Banach space  for which
for which  . An operator
. An operator  that is densely defined in
that is densely defined in  is a generating operator (generator) of the contraction semi-group if and only if the Hille–Yosida condition is satisfied:
is a generating operator (generator) of the contraction semi-group if and only if the Hille–Yosida condition is satisfied:
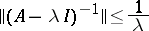 |
for all  . In other words, a densely-defined operator
. In other words, a densely-defined operator 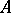 is a generator of a contraction semi-group if and only if is a maximal dissipative operator.
is a generator of a contraction semi-group if and only if is a maximal dissipative operator.
Contraction semi-groups in Hilbert space have been studied in detail. Particular forms of contraction semi-groups are semi-groups of isometries 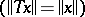 , unitary semi-groups
, unitary semi-groups  , self-adjoint semi-groups
, self-adjoint semi-groups 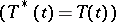 and normal semi-groups
and normal semi-groups 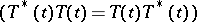 . Instead of the generator
. Instead of the generator  it is sometimes convenient to use its Cayley transform:
it is sometimes convenient to use its Cayley transform: 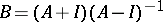 (a cogenerator). It turns out that a semi-group is a semi-group of isometries, or a unitary, a self-adjoint, or a normal semi-group if and only if the cogenerator is, respectively, an isometric, a unitary, a self-adjoint, or a normal operator.
(a cogenerator). It turns out that a semi-group is a semi-group of isometries, or a unitary, a self-adjoint, or a normal semi-group if and only if the cogenerator is, respectively, an isometric, a unitary, a self-adjoint, or a normal operator.
A contraction semi-group is called completely non-unitary, if its restriction to any invariant subspace is not unitary. For a completely non-unitary semi-group 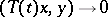 as
as  , for any
, for any 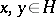 . In order that a contraction semi-group is completely non-unitary it is sufficient that it be stable, that is, that
. In order that a contraction semi-group is completely non-unitary it is sufficient that it be stable, that is, that 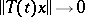 as
as  , for
, for  .
.
For every contraction semi-group 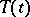 there is an orthogonal decomposition
there is an orthogonal decomposition  into
into 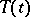 -invariant subspaces such that the semi-group is unitary on
-invariant subspaces such that the semi-group is unitary on 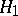 and completely non-unitary on
and completely non-unitary on 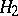 .
.
If 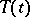 is a contraction semi-group in a Hilbert space
is a contraction semi-group in a Hilbert space 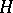 , then there is a larger Hilbert space
, then there is a larger Hilbert space  , containing
, containing 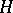 as a subspace, and in it a unitary group
as a subspace, and in it a unitary group  ,
,  , such that
, such that 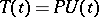 for
for  , where
, where  is the orthogonal projection from
is the orthogonal projection from 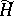 onto
onto  . The group
. The group 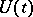 is called a unitary dilation of the semi-group
is called a unitary dilation of the semi-group 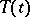 . The dilation is uniquely defined up to an isomorphism if it is required that
. The dilation is uniquely defined up to an isomorphism if it is required that 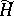 coincides with the closed linear span of the set
coincides with the closed linear span of the set 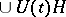 (
(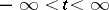 ) (a minimal dilation).
) (a minimal dilation).
Let 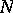 be a Hilbert space and let
be a Hilbert space and let 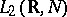 be the Hilbert space of all measurable
be the Hilbert space of all measurable  -valued functions
-valued functions 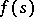 ,
,  , with square-integrable norm. In this space, the unitary group of two-sided shifts,
, with square-integrable norm. In this space, the unitary group of two-sided shifts, 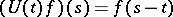 , is defined. Similarly, the semi-group of one-sided shifts is defined in the space
, is defined. Similarly, the semi-group of one-sided shifts is defined in the space 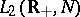 ,
, 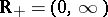 ;
;
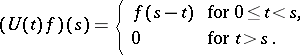 |
Every completely non-unitary semi-group of isometries is isomorphic to the one-sided shift on 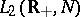 for some suitable space
for some suitable space 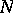 .
.
If  is a completely non-unitary contraction semi-group and
is a completely non-unitary contraction semi-group and 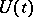 is its minimal unitary dilation, then on some invariant subspace of
is its minimal unitary dilation, then on some invariant subspace of  (but if
(but if  is stable, then on the whole of
is stable, then on the whole of  ) the group is isomorphic to that of two-sided shifts. For contraction semi-groups with non-linear operators, see Semi-group of non-linear operators.
) the group is isomorphic to that of two-sided shifts. For contraction semi-groups with non-linear operators, see Semi-group of non-linear operators.
References
| [1] | E.B. Davies, "One-parameter semigroups" , Acad. Press (1980) |
| [2] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) |
Comments
References
| [a1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [a2] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
Contraction semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction_semi-group&oldid=51663