Continuous functor
From Encyclopedia of Mathematics
A synonym of the concept "functor commuting with limits" . Let 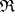 and
and  be categories with limits. A one-place covariant functor
be categories with limits. A one-place covariant functor  is called continuous if
is called continuous if 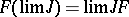 for any diagram
for any diagram 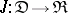 with an arbitrary small diagram scheme
with an arbitrary small diagram scheme  . In more detail, the equality above means the following: If
. In more detail, the equality above means the following: If  is the limit of the diagram
is the limit of the diagram  and
and  ,
, 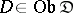 , are morphisms occurring in the definition of limit, then
, are morphisms occurring in the definition of limit, then 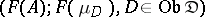 is the limit of the diagram
is the limit of the diagram  .
.
A functor 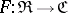 is continuous if and only if it commutes with products of arbitrary families of objects and kernels of pairs of morphisms. Every basic functor
is continuous if and only if it commutes with products of arbitrary families of objects and kernels of pairs of morphisms. Every basic functor 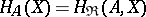 from
from 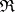 to the category of sets is continuous.
to the category of sets is continuous.
Comments
References
| [a1] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
How to Cite This Entry:
Continuous functor. M.Sh. Tsalenko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_functor&oldid=18119
Continuous functor. M.Sh. Tsalenko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_functor&oldid=18119
This text originally appeared in Encyclopedia of Mathematics - ISBN 1402006098