Continuous analogues of iteration methods
Continuous models that make it possible to study problems concerning the existence of solutions of non-linear equations, to produce by means of the well-developed apparatus of continuous analysis preliminary results on the convergence and optimality of iteration methods, and to obtain new classes of such methods.
One can set up a correspondence between methods for solving stationary problems by adjustment (see Adjustment method) and certain iteration methods (see [1], [2]). For example, for the solution of a linear equation
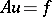 | (1) |
with a positive-definite self-adjoint operator 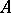 it is known that one-step iteration methods of the form
it is known that one-step iteration methods of the form
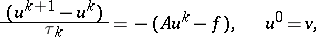 | (2) |
converge for sufficiently small 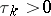 . Introduce a continuous time
. Introduce a continuous time  and regard the quantities
and regard the quantities 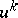 as the values of a certain function
as the values of a certain function  at
at 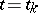 , where
, where
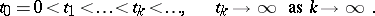 |
If one puts 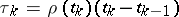 , where
, where  is a continuous function for
is a continuous function for 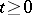 , then in passing to the limit in (2) as
, then in passing to the limit in (2) as 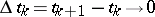 , one obtains a continuous analogue of the iteration method (2):
, one obtains a continuous analogue of the iteration method (2):
 | (3) |
If also
 |
as 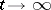 , then
, then 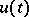 tends to
tends to 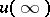 , a solution of (1).
, a solution of (1).
Similarly, with the one-step gradient iteration methods for the minimization of a function 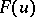 :
:
 | (4) |
one can associate a continuous analogue:
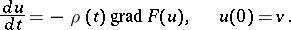 | (5) |
Here the function 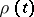 affects only the parametrization of the curve of steepest descent. To solve (1) one may take
affects only the parametrization of the curve of steepest descent. To solve (1) one may take 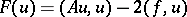 . Then the formulas (4) take the form (2) and the equations (5) the form (3).
. Then the formulas (4) take the form (2) and the equations (5) the form (3).
By means of transformations two-step iteration methods
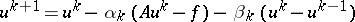 | (6) |
can be brought to the form
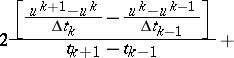 | (7) |
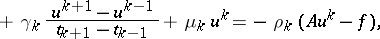 |
where the quantities 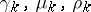 , and
, and 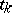 are (non-uniquely) defined in terms of the parameters
are (non-uniquely) defined in terms of the parameters 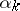 and
and 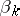 of (6). Taking limits in (7) as
of (6). Taking limits in (7) as  leads to a continuous analogue:
leads to a continuous analogue:
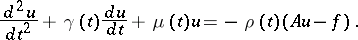 | (8) |
The adjustment method involving an equation like (8) is called the method of the heavy sphere (see [2]). There exist iteration methods for which the continuous analogues contain differential operators of higher orders (see [3]).
A source for obtaining differential equations playing the role of continuous analogues of iteration methods can be the continuation method (with respect to a parameter) (see [4], [5]). In this method, to find a solution of an equation
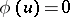 | (9) |
one constructs an equation
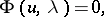 | (10) |
depending on a parameter 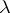 , such that for
, such that for 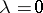 a solution of (10) is known:
a solution of (10) is known: 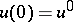 , and such that for
, and such that for 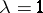 the solutions of (9) and (10) are the same. For example, one can take
the solutions of (9) and (10) are the same. For example, one can take
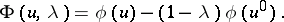 | (11) |
By differentiating (1) with respect to the parameter and taking 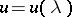 one obtains a differential equation for
one obtains a differential equation for 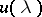 ; for the case (11) it takes the form
; for the case (11) it takes the form
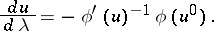 | (12) |
By splitting the interval 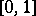 into
into  parts by points
parts by points 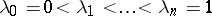 and using for (12) a numerical discretization formula at the points
and using for (12) a numerical discretization formula at the points  (e.g., Euler's method, the Runge–Kutta method, etc.), one obtains recurrence relations between the quantities
(e.g., Euler's method, the Runge–Kutta method, etc.), one obtains recurrence relations between the quantities 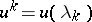 , which one uses to construct the formulas of an iteration method. Thus, after e.g. applying Euler's method, (12) is replaced by the relations
, which one uses to construct the formulas of an iteration method. Thus, after e.g. applying Euler's method, (12) is replaced by the relations
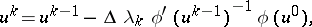 | (13) |
where  , which determine the following two-step iteration method containing internal and external iteration cycles:
, which determine the following two-step iteration method containing internal and external iteration cycles:
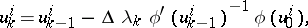 | (14) |
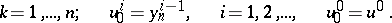 |
For 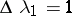 and
and 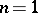 this turns into Newton's classical method. A continuous analogue of Newton's iteration method can also be obtained in another way: In (11) the variable is replaced by
this turns into Newton's classical method. A continuous analogue of Newton's iteration method can also be obtained in another way: In (11) the variable is replaced by 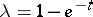 . Then the differential equation (12) takes the form
. Then the differential equation (12) takes the form
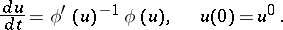 | (15) |
Numerical integration of (15) by Euler's method with respect to the points 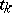 leads to the iteration method
leads to the iteration method
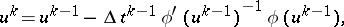 |
which coincides for 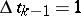 with Newton's classical method.
with Newton's classical method.
Continuous analogues of iteration methods for the solution of boundary value problems for the differential equations of mathematical physics are, as a rule, mixed problems for partial differential equations of a special form (e.g. with rapidly oscillating coefficients or with small coefficients in front of the highest derivatives).
See also Closure of a computational algorithm.
References
| [1] | M.K. Gavurin, "Nonlinear functional equations and continuous analogues of iteration methods" Izv. Vyssh. Uchevn. Zaved. Mat. : 5 (6) (1958) pp. 18–31 (In Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , 1 , MIR (1977) (Translated from Russian) |
| [3] | G.I. Marchuk, V.I. Lebedev, "Numerical methods in the theory of neutron transport" , Harwood (1986) (Translated from Russian) |
| [4] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of nonlinear equations in several variables" , Acad. Press (1970) |
| [5] | D.F. Davidenko, "The iteration method of parameter variation for the inversion of linear operations" Zh. Vychisl. Mat. i. Mat. Fiz. , 15 : 1 (1975) pp. 30–47 (In Russian) |
Comments
References
| [a1] | W.C. Rheinboldt, "Numerical analysis of parametrized nonlinear equations" , Wiley (1986) |
Continuous analogues of iteration methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_analogues_of_iteration_methods&oldid=17493