Continuity theorem
continuity principle
Let 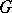 be a domain of holomorphy in
be a domain of holomorphy in  ,
, 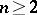 , and let
, and let 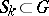 and
and  ,
,  be two sequences of sets, with compact closures in
be two sequences of sets, with compact closures in 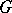 , for which the maximum modulus principle holds for functions
, for which the maximum modulus principle holds for functions 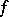 that are holomorphic in
that are holomorphic in  , that is,
, that is,
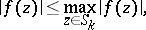 |
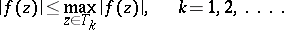 |
Then if 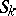 converges to some bounded set
converges to some bounded set 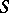 and
and  to a set
to a set 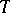 , and if
, and if 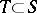 and
and 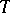 has compact closure in
has compact closure in 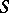 , then
, then 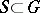 has compact closure in
has compact closure in 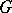 . If for
. If for 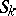 one takes analytic hypersurfaces and for
one takes analytic hypersurfaces and for 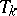 their boundaries
their boundaries 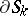 , one obtains the Behnke–Sommer theorem (see [1]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on "analytic discs" . For example, the strong theorem on analytic "discs" asserts the following. Suppose that in
, one obtains the Behnke–Sommer theorem (see [1]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on "analytic discs" . For example, the strong theorem on analytic "discs" asserts the following. Suppose that in 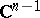 a Jordan curve of the form
a Jordan curve of the form
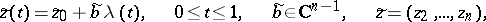 |
is given. Let 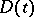 ,
, 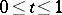 , be a family of domains in the
, be a family of domains in the 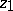 -plane having the property that for any compact set
-plane having the property that for any compact set 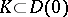 there is a number
there is a number 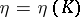 such that
such that 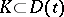 for all
for all 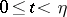 . If
. If 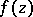 is holomorphic at the points of the "discs"
is holomorphic at the points of the "discs"
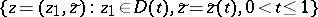 |
and at one point of the limiting "disc"
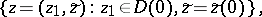 |
then 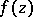 is holomorphic also at all points of the limiting "disc" . Theorems on "analytic discs" are very useful in the holomorphic extension of domains and in constructing envelopes of holomorphy (cf. Holomorphic envelope), for example, in the proof of Bochner's theorem on the envelope of holomorphy of a tube domain, of the Osgood–Brown theorem, and of the theorem on "imbedded edges" , "the edge-of-the-wedge" , "C-convex hulls" , and others. The continuity principles given go back to the Hartogs theorem on removable singularities (1916) for holomorphic functions of several complex variables.
is holomorphic also at all points of the limiting "disc" . Theorems on "analytic discs" are very useful in the holomorphic extension of domains and in constructing envelopes of holomorphy (cf. Holomorphic envelope), for example, in the proof of Bochner's theorem on the envelope of holomorphy of a tube domain, of the Osgood–Brown theorem, and of the theorem on "imbedded edges" , "the edge-of-the-wedge" , "C-convex hulls" , and others. The continuity principles given go back to the Hartogs theorem on removable singularities (1916) for holomorphic functions of several complex variables.
References
| [1] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) (Elraged & Revised Edition. Original: 1934) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
Comments
The continuity principle is also known as Hartogs' Kontinuitätssatz (Hartogs' continuity theorem).
References
| [a1] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Chapt. 3 |
| [a2] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 2 |
Continuity theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuity_theorem&oldid=14214