Difference between revisions of "Continuity theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559011.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559011.png" /></td> </tr></table> | ||
| − | Then if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559012.png" /> converges to some bounded set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559014.png" /> to a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559015.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559017.png" /> has compact closure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559018.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559019.png" /> has compact closure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559020.png" />. If for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559021.png" /> one takes analytic hypersurfaces and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559022.png" /> their boundaries <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559023.png" />, one obtains the Behnke–Sommer theorem (see [[#References|[1]]]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on | + | Then if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559012.png" /> converges to some bounded set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559014.png" /> to a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559015.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559017.png" /> has compact closure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559018.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559019.png" /> has compact closure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559020.png" />. If for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559021.png" /> one takes analytic hypersurfaces and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559022.png" /> their boundaries <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559023.png" />, one obtains the Behnke–Sommer theorem (see [[#References|[1]]]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on "analytic discs" . For example, the strong theorem on analytic "discs" asserts the following. Suppose that in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559024.png" /> a Jordan curve of the form |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559025.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559025.png" /></td> </tr></table> | ||
| − | is given. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559027.png" />, be a family of domains in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559028.png" />-plane having the property that for any compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559029.png" /> there is a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559030.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559031.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559032.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559033.png" /> is holomorphic at the points of the | + | is given. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559027.png" />, be a family of domains in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559028.png" />-plane having the property that for any compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559029.png" /> there is a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559030.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559031.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559032.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559033.png" /> is holomorphic at the points of the "discs" |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559034.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559034.png" /></td> </tr></table> | ||
| − | and at one point of the limiting | + | and at one point of the limiting "disc" |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559035.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559035.png" /></td> </tr></table> | ||
| − | then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559036.png" /> is holomorphic also at all points of the limiting | + | then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025590/c02559036.png" /> is holomorphic also at all points of the limiting "disc" . Theorems on "analytic discs" are very useful in the holomorphic extension of domains and in constructing envelopes of holomorphy (cf. [[Holomorphic envelope|Holomorphic envelope]]), for example, in the proof of Bochner's theorem on the envelope of holomorphy of a tube domain, of the Osgood–Brown theorem, and of the theorem on "imbedded edges" , "the edge-of-the-wedge" , "C-convex hulls" , and others. The continuity principles given go back to the [[Hartogs theorem|Hartogs theorem]] on removable singularities (1916) for holomorphic functions of several complex variables. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) (Elraged & Revised Edition. Original: 1934)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''2''' , Moscow (1976) (In Russian) {{MR|}} {{ZBL|0799.32001}} {{ZBL|0732.32001}} {{ZBL|0732.30001}} {{ZBL|0578.32001}} {{ZBL|0574.30001}} </TD></TR></table> |
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Chapt. 3 {{MR|0635928}} {{ZBL|0471.32008}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 2 {{MR|0847923}} {{ZBL|}} </TD></TR></table> |
Latest revision as of 16:56, 15 April 2012
continuity principle
Let 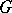 be a domain of holomorphy in
be a domain of holomorphy in  ,
, 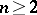 , and let
, and let 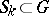 and
and  ,
,  be two sequences of sets, with compact closures in
be two sequences of sets, with compact closures in 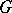 , for which the maximum modulus principle holds for functions
, for which the maximum modulus principle holds for functions 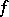 that are holomorphic in
that are holomorphic in  , that is,
, that is,
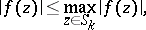 |
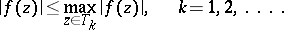 |
Then if 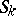 converges to some bounded set
converges to some bounded set 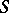 and
and  to a set
to a set 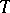 , and if
, and if 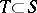 and
and 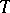 has compact closure in
has compact closure in 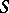 , then
, then 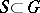 has compact closure in
has compact closure in 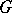 . If for
. If for 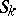 one takes analytic hypersurfaces and for
one takes analytic hypersurfaces and for 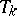 their boundaries
their boundaries 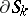 , one obtains the Behnke–Sommer theorem (see [1]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on "analytic discs" . For example, the strong theorem on analytic "discs" asserts the following. Suppose that in
, one obtains the Behnke–Sommer theorem (see [1]). Hence it follows that every domain of holomorphy is pseudo-convex. Applied to a specific function, certain modifications of the continuity theorem are known as theorems on "analytic discs" . For example, the strong theorem on analytic "discs" asserts the following. Suppose that in 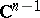 a Jordan curve of the form
a Jordan curve of the form
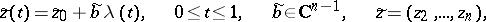 |
is given. Let 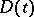 ,
, 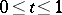 , be a family of domains in the
, be a family of domains in the 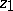 -plane having the property that for any compact set
-plane having the property that for any compact set 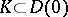 there is a number
there is a number 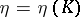 such that
such that 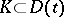 for all
for all 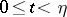 . If
. If 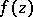 is holomorphic at the points of the "discs"
is holomorphic at the points of the "discs"
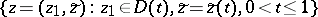 |
and at one point of the limiting "disc"
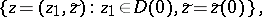 |
then 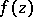 is holomorphic also at all points of the limiting "disc" . Theorems on "analytic discs" are very useful in the holomorphic extension of domains and in constructing envelopes of holomorphy (cf. Holomorphic envelope), for example, in the proof of Bochner's theorem on the envelope of holomorphy of a tube domain, of the Osgood–Brown theorem, and of the theorem on "imbedded edges" , "the edge-of-the-wedge" , "C-convex hulls" , and others. The continuity principles given go back to the Hartogs theorem on removable singularities (1916) for holomorphic functions of several complex variables.
is holomorphic also at all points of the limiting "disc" . Theorems on "analytic discs" are very useful in the holomorphic extension of domains and in constructing envelopes of holomorphy (cf. Holomorphic envelope), for example, in the proof of Bochner's theorem on the envelope of holomorphy of a tube domain, of the Osgood–Brown theorem, and of the theorem on "imbedded edges" , "the edge-of-the-wedge" , "C-convex hulls" , and others. The continuity principles given go back to the Hartogs theorem on removable singularities (1916) for holomorphic functions of several complex variables.
References
| [1] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) (Elraged & Revised Edition. Original: 1934) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) Zbl 0799.32001 Zbl 0732.32001 Zbl 0732.30001 Zbl 0578.32001 Zbl 0574.30001 |
Comments
The continuity principle is also known as Hartogs' Kontinuitätssatz (Hartogs' continuity theorem).
References
| [a1] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Chapt. 3 MR0635928 Zbl 0471.32008 |
| [a2] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 2 MR0847923 |
Continuity theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuity_theorem&oldid=14214