Continued fraction
An expression of the form
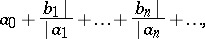 | (1) |
where
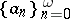 | (2) |
and
 | (3) |
are finite or infinite sequences of complex numbers. Instead of the expression (1) one also uses the notation
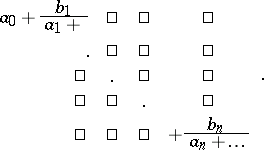 |
The continued fraction of the sequence (2) is defined as the expression
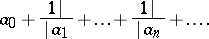 |
For every continued fraction (1) the recurrence equations
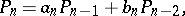 |
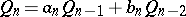 |
with the initial conditions
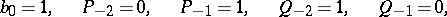 |
determine two sequences 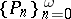 and
and 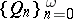 of complex numbers. As a rule, it is assumed that the sequences (2) and (3) are such that
of complex numbers. As a rule, it is assumed that the sequences (2) and (3) are such that 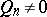 for all
for all  ,
, 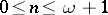 . The fraction
. The fraction 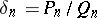 is called the
is called the  -th convergent of the continued fraction (1). Here
-th convergent of the continued fraction (1). Here
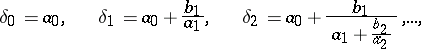 |
moreover,
 |
It is convenient to denote the  -th convergent of the continued fraction of the sequence (2) by
-th convergent of the continued fraction of the sequence (2) by
 |
These convergents satisfy the following equalities:
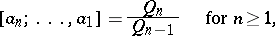 |
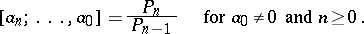 |
If  and the sequence of convergents of (1) converges to some limit
and the sequence of convergents of (1) converges to some limit 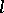 , then the continued fraction (1) is called convergent and the number
, then the continued fraction (1) is called convergent and the number 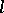 is its value. If
is its value. If 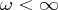 , that is, the continued fraction is finite, then its value is defined as the last of its convergents.
, that is, the continued fraction is finite, then its value is defined as the last of its convergents.
If all terms of the sequences (2) and (3), except possibly  , are positive real numbers, and if
, are positive real numbers, and if 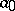 is real, then the sequence
is real, then the sequence 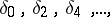 of convergents of even order of (1) increases, and the sequence
of convergents of even order of (1) increases, and the sequence 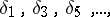 of convergents of odd order decreases. Here a convergent of even order is less than the corresponding convergent of odd order (see [5]).
of convergents of odd order decreases. Here a convergent of even order is less than the corresponding convergent of odd order (see [5]).
If 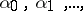 is the sequence of complex numbers for which
is the sequence of complex numbers for which
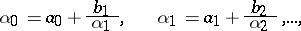 |
then the expression (1) is called an expansion of the number  in a continued fraction. Not every continued fraction converges, and the value of a continued fraction is not always equal to the number from which it is expanded. There are a number of criteria for the convergence of continued fractions (see, for example, [3] and [5]):
in a continued fraction. Not every continued fraction converges, and the value of a continued fraction is not always equal to the number from which it is expanded. There are a number of criteria for the convergence of continued fractions (see, for example, [3] and [5]):
1) Suppose that  , that all terms of the sequences (2) and (3) are real numbers, and that
, that all terms of the sequences (2) and (3) are real numbers, and that 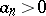 for all natural numbers
for all natural numbers  from some term onwards. If
from some term onwards. If 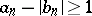 for such
for such  , then the continued fraction (1) converges.
, then the continued fraction (1) converges.
2) Suppose that 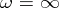 and that all terms of the sequence (2) beginning with
and that all terms of the sequence (2) beginning with 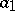 are positive. Then the continued fraction of the sequence (2) converges if and only if the series
are positive. Then the continued fraction of the sequence (2) converges if and only if the series  diverges (Seidel's theorem).
diverges (Seidel's theorem).
The continued fraction of a sequence (2) is called regular if all its terms (except possibly 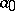 ) are natural numbers,
) are natural numbers, 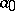 is an integer and
is an integer and 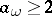 for
for 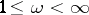 . For every real number
. For every real number  there exists a unique regular continued fraction with value
there exists a unique regular continued fraction with value  . This fraction is finite if and only if
. This fraction is finite if and only if  is rational (see [1], [2], [4]). An algorithm for the expansion of a real number
is rational (see [1], [2], [4]). An algorithm for the expansion of a real number  in a regular continued fraction is defined by the following relations
in a regular continued fraction is defined by the following relations
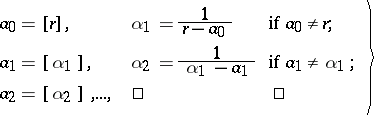 | (4) |
where 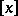 denotes the integral part of
denotes the integral part of  .
.
The numbers 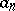 and
and 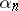 defined by (4) are called, respectively, the complete and incomplete quotients of order
defined by (4) are called, respectively, the complete and incomplete quotients of order  of the expansion of
of the expansion of  in a continued fraction.
in a continued fraction.
Around 1768 J. Lambert found the expansion of 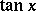 in a continued fraction:
in a continued fraction:
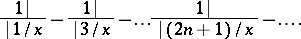 |
Under the assumption that this continued fraction converges, A. Legendre proved that its value for rational values of  is irrational. It should be mentioned that in this way he proved the irrationality of the number
is irrational. It should be mentioned that in this way he proved the irrationality of the number 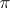 (see [7]).
(see [7]).
L. Euler found in 1737 that
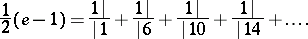 |
A real number  is an irrational root of a polynomial of degree 2 with integer coefficients if and only of the incomplete quotients of the expansion of
is an irrational root of a polynomial of degree 2 with integer coefficients if and only of the incomplete quotients of the expansion of  in a continued fraction from some term onwards are repeated periodically (the Euler–Lagrange theorem, see [1] and [4]). At present (1984) expansions in regular continued fractions of algebraic numbers of degree 3 and higher are not known. The assertion that the incomplete quotients of the expansion of
in a continued fraction from some term onwards are repeated periodically (the Euler–Lagrange theorem, see [1] and [4]). At present (1984) expansions in regular continued fractions of algebraic numbers of degree 3 and higher are not known. The assertion that the incomplete quotients of the expansion of 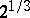 in a continued fraction are bounded has not been proved.
in a continued fraction are bounded has not been proved.
Regular continued fractions are a very convenient tool for the approximation of real numbers by rational numbers. The following propositions hold:
1) If  and
and 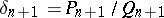 are neighbouring convergents of the expansion of a number
are neighbouring convergents of the expansion of a number  in a regular continued fraction, then
in a regular continued fraction, then
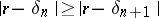 |
and
 |
where in the latter case equality holds only when 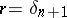 .
.
2) For two neighbouring convergents of the expansion of a number  in a regular continued fraction, at least one of them satisfies the inequality:
in a regular continued fraction, at least one of them satisfies the inequality:
 |
3) If  and
and 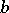 are integers,
are integers, 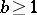 , if
, if  is a real number, and if
is a real number, and if
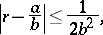 |
then 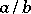 is a convergent of the expansion of
is a convergent of the expansion of  in a regular continued fraction.
in a regular continued fraction.
4) If 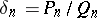 is a convergent of the expansion of a number
is a convergent of the expansion of a number  into a regular continued fraction, then for any integers
into a regular continued fraction, then for any integers  and
and  it follows from
it follows from 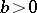 ,
,  and
and
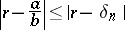 |
that 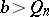 (theorem on the best approximation).
(theorem on the best approximation).
The first twenty-five incomplete quotients of the expansion of the number 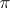 in a regular continued fraction are: 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1.
in a regular continued fraction are: 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1.
The first five convergents of the expansion of  in a regular continued fraction are:
in a regular continued fraction are:
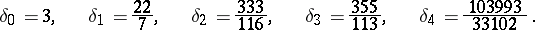 |
Therefore,
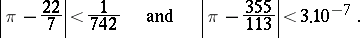 |
There exist several generalizations of continued fractions (see, e.g., [9]).
References
| [1] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [2] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [3] | A.A. Markov, "Selected works" , Moscow-Leningrad (1948) (In Russian) |
| [4] | A.Ya. [A.Ya. Khinchin] Khintchine, "Kettenbrüche" , Teubner (1956) (Translated from Russian) |
| [5] | A.N. Khovanskii, "Application of continued fractions and their generalizations to problems in approximation theory" , Moscow (1966) (In Russian) |
| [6] | , The history of mathematics from Antiquity to the beginning of the XIX-th century , 3 , Moscow (1972) (In Russian) |
| [7] | , Ueber die Kwadratur des Kreises (1936) |
| [8] | O. Perron, "Die Lehre von den Kettenbrüchen" , 1–2 , Teubner (1954–1957) |
| [9] | G. Szekeres, "Multidimensional continued fractions" Ann. Univ. Sci. Sec. Math. , 13 (1970) pp. 113–140 |
| [10] | W.B. Jones, W.J. Thron, "Continued fractions, analytic theory and applications" , Addison-Wesley (1980) |
Comments
A classical reference on convergence is [a1]. Together with [10], recent references are [a2]–[a4]. Some generalizations can be found in [a5]–[a7]. Except for [a1], [a8] all references contain extensive lists of references on recent developments and applications in Padé approximation; moment problems (cf. Moment problem); orthogonal polynomials; number theory; and the metrical theory of continued fractions (see also Metric theory of numbers).
References
| [a1] | H.S. Wall, "Analytic theory of continued fractions" , Chelsea (1973) |
| [a2] | W.B. Jones (ed.) W.J. Thron (ed.) E.H. Waadeland (ed.) , Analytic theory of continued fractions , Lect. notes in math. , 932 , Springer (1982) |
| [a3] | W.J. Thron (ed.) , Analytic theory of continued fractions II , Lect. notes in math. , 1199 , Springer (1986) |
| [a4] | C. Kraaikamp, "The distribution of some sequences connected with the nearest integer continued fraction" Indag. Math. , 49 (1987) pp. 177–191 |
| [a5] | A.J. Brentjes, "Multidimensional continued fractions" , CWI , Amsterdam (1981) |
| [a6] | V.Ya. Skorobogatko, "The theory of convergent continued fractions and its applications in numerical mathematics" , Moscow (1983) (In Russian) |
| [a7] | D.I. Bodnap, "Convergent continued fractions" , Kiev (1986) (In Russian) |
| [a8] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1959) |
| [a9] | P. Henrici, "Applied and computational complex analysis" , 2 , Wiley (1977) |
Continued fraction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continued_fraction&oldid=30343