Constructible subset

of an algebraic variety

A finite union of locally closed (in the Zariski topology) subsets. A locally closed subset is, by definition, an intersection of an open and a closed subset. The constructible subsets form a Boolean algebra and can be defined as elements of the Boolean algebra generated by the algebraic subvarieties. The role of constructible subsets in algebraic geometry is revealed by Chevalley's theorem: If 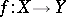is a morphism of algebraic varieties, then 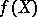(and, moreover, the image of any constructible subset in 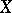) is a constructible subset in 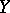. This is related to the fact that "algebraic" conditions determine the constructible subsets of an algebraic variety.

A mapping 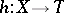is called constructible if 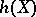is finite and if for any point 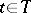the pre-image 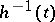is a constructible subset in .

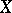References

[1]	A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971)
[2]	A. Borel, "Linear algebraic groups" , Benjamin (1969)