Consistent test
consistent statistical test
A statistical test that reliably distinguishes a hypothesis to be tested from an alternative by increasing the number of observations to infinity.
Let 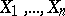 be a sequence of independent identically-distributed random variables taking values in a sample space
be a sequence of independent identically-distributed random variables taking values in a sample space  ,
, 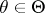 , and suppose one is testing the hypothesis
, and suppose one is testing the hypothesis 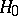 :
: 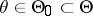 against the alternative
against the alternative 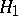 :
: 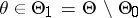 , with an error of the first kind (see Significance level) being given in advance and equal to
, with an error of the first kind (see Significance level) being given in advance and equal to 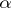 (
( ). Suppose that the first
). Suppose that the first  observations
observations 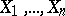 are used to construct a statistical test of level
are used to construct a statistical test of level 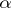 for testing
for testing 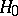 against
against 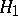 , and let
, and let 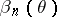 ,
, 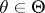 , be its power function (cf. Power function of a test), which gives for every
, be its power function (cf. Power function of a test), which gives for every 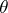 the probability that this test rejects
the probability that this test rejects 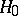 when the random variable
when the random variable 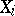 is subject to the law
is subject to the law 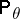 . Of course
. Of course 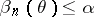 for all
for all 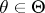 . By increasing the number of observations without limit it is possible to construct a sequence of statistical tests of a prescribed level
. By increasing the number of observations without limit it is possible to construct a sequence of statistical tests of a prescribed level 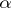 intended to test
intended to test 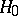 against
against 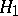 ; the corresponding sequence of power functions
; the corresponding sequence of power functions 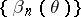 satisfies the condition
satisfies the condition
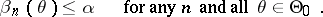 |
If under these conditions the sequence of power functions 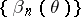 is such that, for any fixed
is such that, for any fixed 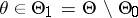 ,
,
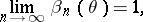 |
then one says that a consistent sequence of statistical tests of level 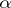 has been constructed for testing
has been constructed for testing 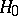 against
against  . With a certain amount of license, one says that a consistent test has been constructed. Since
. With a certain amount of license, one says that a consistent test has been constructed. Since 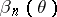 ,
, 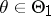 (which is the restriction of
(which is the restriction of 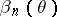 ,
, 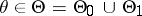 , to
, to 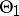 ), is the power of the statistical test constructed from the observations
), is the power of the statistical test constructed from the observations 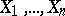 , the property of consistency of a sequence of statistical tests can be expressed as follows: The corresponding powers
, the property of consistency of a sequence of statistical tests can be expressed as follows: The corresponding powers 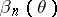 ,
, 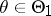 , converge on
, converge on 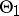 to the function identically equal to 1 on
to the function identically equal to 1 on 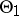 .
.
Example. Let 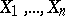 be independent identically-distributed random variables whose distribution function belongs to the family
be independent identically-distributed random variables whose distribution function belongs to the family 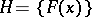 of all continuous distribution functions on
of all continuous distribution functions on 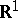 , and let
, and let 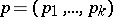 be a vector of positive probabilities such that
be a vector of positive probabilities such that 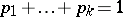 . Further, let
. Further, let 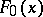 be any distribution function of
be any distribution function of 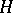 . Then
. Then 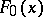 and
and 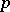 uniquely determine a partition of the real axis into
uniquely determine a partition of the real axis into 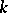 intervals
intervals 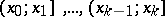 , where
, where
 |
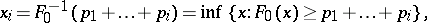 |
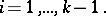 |
In other words, the end points of the intervals are quantiles of the distribution function 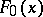 . These intervals determine a partition of
. These intervals determine a partition of 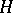 into two disjoint sets
into two disjoint sets 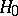 and
and 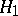 as follows: A distribution function
as follows: A distribution function 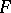 of
of 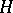 belongs to
belongs to 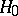 if and only if
if and only if
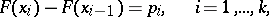 |
and otherwise 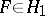 . Now let
. Now let  be the vector of counts obtained as a result of grouping the first
be the vector of counts obtained as a result of grouping the first  random variables
random variables 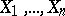 (
(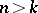 ) into the intervals
) into the intervals 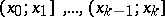 . Then to test the hypothesis
. Then to test the hypothesis 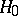 that the distribution function of the
that the distribution function of the 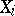 belongs to the set
belongs to the set 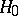 against the alternative
against the alternative 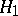 that it belongs to the set
that it belongs to the set 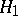 , one can make use of the "chi-squared" test based on the statistic
, one can make use of the "chi-squared" test based on the statistic
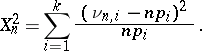 |
According to this, with significance level 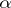 (
(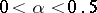 ), the hypothesis
), the hypothesis  must be rejected whenever
must be rejected whenever 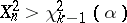 , where
, where 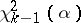 is the upper
is the upper 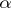 -quantile of the "chi-squared" distribution with
-quantile of the "chi-squared" distribution with 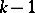 degrees of freedom. From the general theory of tests of "chi-squared" type it follows that when
degrees of freedom. From the general theory of tests of "chi-squared" type it follows that when 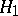 is correct,
is correct,
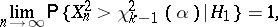 |
which also shows the consistency of the "chi-squared" test for testing 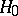 against
against 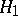 . But if one takes an arbitrary non-empty subset of
. But if one takes an arbitrary non-empty subset of 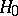 and considers the problem of testing against the alternative
and considers the problem of testing against the alternative 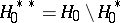 , then it is clear that the "chi-squared" sequence of tests based on the statistics
, then it is clear that the "chi-squared" sequence of tests based on the statistics 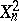 is not consistent, since
is not consistent, since
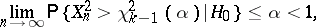 |
and, in particular,
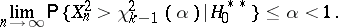 |
References
| [1] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
| [2] | E. Lehman, "Testing statistical hypotheses" , Wiley (1959) |
Consistent test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Consistent_test&oldid=12096