Connes-Moscovici index theorem
Gamma index theorem,  index theorem
index theorem
A theorem [a3] which computes the pairing of a cyclic cocycle  of the group algebra
of the group algebra  with the algebraic
with the algebraic  -theory index of an invariant (pseudo-) differential operator on a covering
-theory index of an invariant (pseudo-) differential operator on a covering  with Galois group (or group of deck transformations)
with Galois group (or group of deck transformations)  (cf. also Cohomology).
(cf. also Cohomology).
The ingredients of this theorem are stated in more detail below. Let  be a smooth compact manifold.
be a smooth compact manifold.
First, any  -invariant, elliptic partial differential operator (cf. Elliptic partial differential equation)
-invariant, elliptic partial differential operator (cf. Elliptic partial differential equation)  on
on 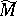 has an algebraic
has an algebraic  -theory index
-theory index  . The definition of
. The definition of  is obtained using the boundary mapping on
is obtained using the boundary mapping on  applied to
applied to 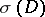 , the principal symbol of
, the principal symbol of 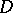 (cf. also Symbol of an operator). This gives
(cf. also Symbol of an operator). This gives
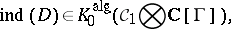 |
where 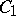 is the algebra of trace-class operators on
is the algebra of trace-class operators on 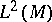 (cf. also Trace). More generally, one can assume that
(cf. also Trace). More generally, one can assume that 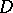 is an invariant pseudo-differential operator on
is an invariant pseudo-differential operator on 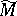 (with nice support).
(with nice support).
Secondly, it is known [a2] that any group-cohomology 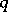 -cocycle
-cocycle 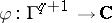 of
of 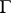 can be represented by an anti-symmetric function, and hence it defines a cyclic cocycle on the group algebra
can be represented by an anti-symmetric function, and hence it defines a cyclic cocycle on the group algebra 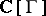 of the group
of the group  . Moreover, the class of this cocycle in the periodic cyclic cohomology group
. Moreover, the class of this cocycle in the periodic cyclic cohomology group  , also denoted by
, also denoted by 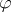 , depends only on the class of
, depends only on the class of 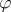 in
in  . Here, as customary,
. Here, as customary,  denotes the classifying space of
denotes the classifying space of  , whose simplicial cohomology is known to be isomorphic to
, whose simplicial cohomology is known to be isomorphic to 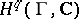 , the group cohomology of
, the group cohomology of  .
.
Finally, any element 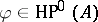 gives rise to a group morphism
gives rise to a group morphism  , see [a2]. In particular, any group cocycle
, see [a2]. In particular, any group cocycle  gives rise to a mapping
gives rise to a mapping
 |
using also the trace on  .
.
The Connes–Moscovici index theorem now states [a3]): Let 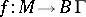 be the mapping classifying the covering
be the mapping classifying the covering  , let
, let 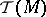 be the Todd class of
be the Todd class of 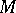 , and let
, and let  be the Chern character of the element in
be the Chern character of the element in  defined by
defined by 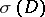 , as in the Atiyah–Singer index theorem (see [a1] and Index formulas). Then
, as in the Atiyah–Singer index theorem (see [a1] and Index formulas). Then
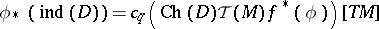 |
is a pairing of a compactly supported cohomology class with the fundamental class of  . Here,
. Here, 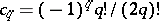 .
.
The Connes–Moscovici index theorem is sometimes called the higher index theorem for coverings and is the prototype of a higher index theorem.
References
| [a1] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. , 93 (1971) pp. 484–530 |
| [a2] | A. Connes, "Non-commutative differential geometry" Publ. Math. IHES , 62 (1985) pp. 41–144 |
| [a3] | A. Connes, H. Moscovici, "Cyclic cohomology, the Novikov conjecture and hyperbolic groups" Topology , 29 (1990) pp. 345–388 |
| [a4] | G. Lusztig, "Novikov's higher signature and families of elliptic operators" J. Diff. Geom. , 7 (1972) pp. 229–256 |
Connes-Moscovici index theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Connes-Moscovici_index_theorem&oldid=13937