Connection object
A differential-geometric object on a smooth principal fibre bundle  that is used to define a horizontal distribution
that is used to define a horizontal distribution  of a connection in
of a connection in  . Let
. Let  be the bundle of all tangent frames to
be the bundle of all tangent frames to  such that the first
such that the first  vectors
vectors  are tangent to the corresponding fibre, and are generated by
are tangent to the corresponding fibre, and are generated by  basis elements in the Lie algebra of the structure group
basis elements in the Lie algebra of the structure group  of
of  ,
,  . A connection object then consists of functions
. A connection object then consists of functions  on
on  such that the subspace of
such that the subspace of 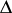 is spanned by the vectors
is spanned by the vectors 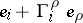
 . Furthermore, the
. Furthermore, the 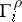 must satisfy the following conditions on
must satisfy the following conditions on 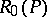 :
:
 | (1) |
They are expressed by using the 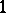 -forms on
-forms on  that occur in the structure equations for the forms
that occur in the structure equations for the forms 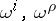 given by the co-basis dual to
given by the co-basis dual to 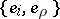 ;
;
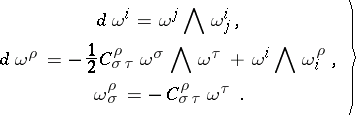 | (2) |
A connection object also defines a corresponding connection form  , given by the relation
, given by the relation  , and its curvature form
, and its curvature form  , given by the formulas:
, given by the formulas:
 |
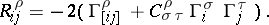 |
For example, let 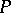 be the space of affine tangent frames of an
be the space of affine tangent frames of an  -dimensional smooth manifold
-dimensional smooth manifold  . Then the second equation in (2) has the form
. Then the second equation in (2) has the form
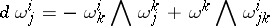 |
and (1) reduces to
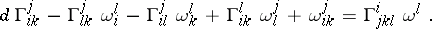 |
Under parallel displacement one must have 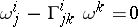 . If a local chart is chosen in
. If a local chart is chosen in 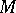 , and if in its domain one makes the transition to the natural frame of the chart, i.e.
, and if in its domain one makes the transition to the natural frame of the chart, i.e.  , then the parallel displacement is defined by
, then the parallel displacement is defined by  . The classical definition of a connection object of an affine connection on
. The classical definition of a connection object of an affine connection on  is given by the set of functions
is given by the set of functions 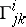 defined on the domains of the charts such that under transition to the coordinates of another chart these functions are transformed according to the formulas
defined on the domains of the charts such that under transition to the coordinates of another chart these functions are transformed according to the formulas
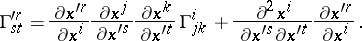 |
Here this follows from the condition of invariance under displacement.
Connection object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Connection_object&oldid=13997