Connection form
A linear differential form 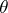 on a principal fibre bundle
on a principal fibre bundle  that takes values in the Lie algebra
that takes values in the Lie algebra  of the structure group
of the structure group 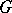 of
of  . It is defined by a certain linear connection
. It is defined by a certain linear connection 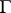 on
on  , and it determines this connection uniquely. The values of the connection form
, and it determines this connection uniquely. The values of the connection form 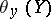 in terms of
in terms of  , where
, where 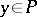 and
and 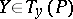 , are defined as the elements of
, are defined as the elements of 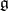 which, under the action of
which, under the action of 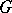 on
on 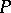 , generate the second component of
, generate the second component of 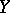 relative to the direct sum
relative to the direct sum 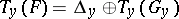 . Here
. Here 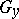 is the fibre of
is the fibre of 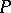 that contains
that contains 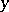 and
and  is the horizontal distribution of
is the horizontal distribution of 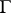 . The horizontal distribution
. The horizontal distribution  , and so the connection
, and so the connection 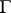 , can be recovered from the connection form
, can be recovered from the connection form 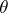 in the following way.
in the following way.
The Cartan–Laptev theorem. For a form 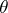 on
on 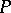 with values in
with values in 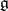 to be a connection form it is necessary and sufficient that: 1)
to be a connection form it is necessary and sufficient that: 1) 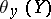 , for
, for 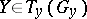 , is the element of
, is the element of 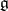 that generates
that generates 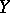 under the action of
under the action of 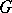 on
on 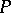 ; and 2) the
; and 2) the  -valued
-valued  -form
-form
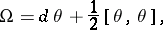 |
formed from 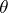 , is semi-basic, or horizontal, that is,
, is semi-basic, or horizontal, that is,  if at least one of the vectors
if at least one of the vectors 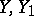 belongs to
belongs to 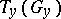 . The
. The  -form
-form  is called the curvature form of the connection. If a basis
is called the curvature form of the connection. If a basis 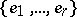 is defined in
is defined in 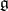 , then condition 2) can locally be expressed by the equalities:
, then condition 2) can locally be expressed by the equalities:
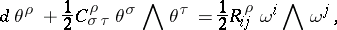 |
where  are certain linearly independent semi-basic
are certain linearly independent semi-basic 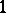 -forms. The necessity of condition 2) was established in this form by E. Cartan [1]; its sufficiency under the additional assumption of 1) was proved by G.F. Laptev [2]. The equations
-forms. The necessity of condition 2) was established in this form by E. Cartan [1]; its sufficiency under the additional assumption of 1) was proved by G.F. Laptev [2]. The equations
for the components of the connection form are called the structure equations for the connection in  , the
, the  define the curvature object.
define the curvature object.
As an example, let  be the space of affine frames in the tangent bundle of an
be the space of affine frames in the tangent bundle of an  -dimensional smooth manifold
-dimensional smooth manifold 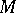 . Then
. Then 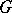 and
and 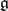 are, respectively, the group and the Lie algebra of matrices of the form
are, respectively, the group and the Lie algebra of matrices of the form
 |
and
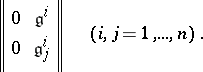 |
By the Cartan–Laptev theorem, the 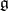 -valued
-valued 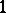 -form
-form
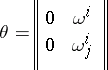 |
on  is the connection form of a certain affine connection on
is the connection form of a certain affine connection on  if and only if
if and only if
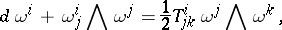 |
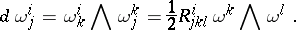 |
Here 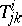 and
and 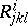 form, respectively, the torsion and curvature tensors of the affine connection on
form, respectively, the torsion and curvature tensors of the affine connection on  . The last two equations for the components of the connection form are called the structure equations for the affine connection on
. The last two equations for the components of the connection form are called the structure equations for the affine connection on 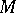 .
.
References
| [1] | E. Cartan, "Espaces à connexion affine, projective et conforme" Acta Math. , 48 (1926) pp. 1–42 |
| [2] | G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigations" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian) |
| [3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
Connection form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Connection_form&oldid=13808