Connected component of the identity
identity component, of a group 
The largest connected subset  of the topological (or algebraic) group
of the topological (or algebraic) group  that contains the identity element of this group. The component
that contains the identity element of this group. The component  is a closed normal subgroup of
is a closed normal subgroup of  ; the cosets with respect to
; the cosets with respect to  coincide with the connected components of
coincide with the connected components of  . The quotient group
. The quotient group  is totally disconnected and Hausdorff, and
is totally disconnected and Hausdorff, and  is the smallest among the normal subgroups
is the smallest among the normal subgroups 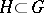 such that
such that  is totally disconnected. If
is totally disconnected. If 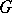 is locally connected (for example, if
is locally connected (for example, if  is a Lie group), then
is a Lie group), then 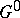 is open in
is open in  and
and 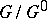 is discrete.
is discrete.
In an arbitrary algebraic group  the identity component
the identity component 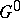 is also open and has finite index; also,
is also open and has finite index; also,  is the minimal closed subgroup of finite index in
is the minimal closed subgroup of finite index in 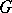 . The connected components of an algebraic group
. The connected components of an algebraic group  coincide with the irreducible components. For every polynomial homomorphism
coincide with the irreducible components. For every polynomial homomorphism  of algebraic groups one has
of algebraic groups one has 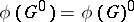 . If
. If  is defined over a field, then
is defined over a field, then  is defined over this field.
is defined over this field.
If 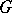 is an algebraic group over the field
is an algebraic group over the field  , then its identity component
, then its identity component  coincides with the identity component of
coincides with the identity component of 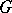 considered as a complex Lie group. If
considered as a complex Lie group. If 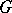 is defined over
is defined over 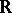 , then the group
, then the group  of real points in
of real points in 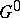 is not necessarily connected in the topology of the Lie group
is not necessarily connected in the topology of the Lie group 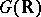 , but the number of its connected components is finite. For example, the group
, but the number of its connected components is finite. For example, the group  splits into two components, although
splits into two components, although  is connected. The pseudo-orthogonal unimodular group
is connected. The pseudo-orthogonal unimodular group 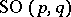 , which can be regarded as the group of real points of the connected complex algebraic group
, which can be regarded as the group of real points of the connected complex algebraic group 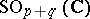 , is connected for
, is connected for 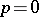 or
or 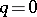 , and splits into two components for
, and splits into two components for 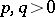 . However, if the Lie group
. However, if the Lie group 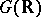 is compact, then
is compact, then 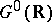 is connected.
is connected.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [3] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
| [4] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Connected component of the identity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Connected_component_of_the_identity&oldid=19121