Conjunctive normal form

A propositional formula of the form

(*)

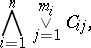where each , ; , is either an atomic formula (a variable or constant) or the negation of an atomic formula. The conjunctive normal form (*) is a tautology if and only if for any one can find both formulas and among the , for some atomic formula . Given any propositional formula , one can construct a conjunctive normal form 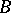equivalent to it and containing the same variables and constants as . This 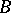is called the conjunctive normal form of .

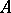Comments

The dual of a conjunctive normal form is a disjunctive normal form. Both are also used in the theory of Boolean functions (cf. Boolean functions, normal forms of).