Conjugate gradients, method of
conjugate-gradient method
A method of solving a system of linear algebraic equations  where
where  is a positive-definite (symmetric) matrix. This is at the same time a direct and an iterative method: for any initial approximation, it converges after a finite number of iterations to give the exact solution. In this method the matrix of the system does not change in the process of calculation and at every iteration it is only used to multiply a vector. Therefore, the order of systems that can be solved on computers is high, being determined by the amount of numerical information needed to specify the matrix.
is a positive-definite (symmetric) matrix. This is at the same time a direct and an iterative method: for any initial approximation, it converges after a finite number of iterations to give the exact solution. In this method the matrix of the system does not change in the process of calculation and at every iteration it is only used to multiply a vector. Therefore, the order of systems that can be solved on computers is high, being determined by the amount of numerical information needed to specify the matrix.
As a direct method, its structure is based on the process of sequential  -orthogonalization of a set of vectors, and is an ordinary orthogonalization process (see Orthogonalization method) with respect to the scalar product
-orthogonalization of a set of vectors, and is an ordinary orthogonalization process (see Orthogonalization method) with respect to the scalar product  . If
. If  is an
is an  -orthogonal basis of the space, then for any initial approximation
-orthogonal basis of the space, then for any initial approximation  , the exact solution
, the exact solution  of the system can be obtained from the decomposition
of the system can be obtained from the decomposition
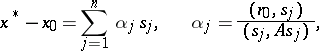 |
where 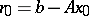 is the discrepancy of
is the discrepancy of  . In the conjugate-gradient method, the
. In the conjugate-gradient method, the 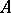 -orthogonal vectors
-orthogonal vectors  are constructed by
are constructed by  -orthogonalizing the discrepancies
-orthogonalizing the discrepancies 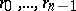 of the sequence of approximations
of the sequence of approximations 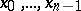 , given by the formulas
, given by the formulas
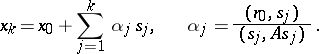 |
The vectors  and
and  constructed in this way have the following properties:
constructed in this way have the following properties:
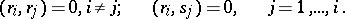 | (1) |
The conjugate-gradient method is now defined by the following recurrence relations (see [1]):
 | (2) |
The process ends at some  for which
for which 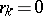 . Then
. Then 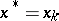 . The cut-off point is determined by the initial approximation
. The cut-off point is determined by the initial approximation 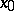 . It follows from the recurrence relations (2) that the vectors
. It follows from the recurrence relations (2) that the vectors  are linear combinations of the vectors
are linear combinations of the vectors 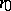 ,
, 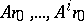 . Since the vectors
. Since the vectors  are orthogonal,
are orthogonal, 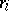 can only vanish when the vectors
can only vanish when the vectors 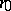 ,
, 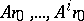 are linearly dependent, as occurs for example when there are only
are linearly dependent, as occurs for example when there are only 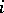 non-zero components in the decomposition of
non-zero components in the decomposition of 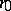 with respect to a basis of eigen vectors of
with respect to a basis of eigen vectors of 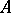 . This consideration can influence the choice of initial approximation.
. This consideration can influence the choice of initial approximation.
The conjugate-gradient method is related to a class of methods in which for a solution a vector that minimizes some functional is taken. To calculate this vector an iterated sequence is constructed that converges to the minimum point. The sequence  in (2) realizes a minimization of the functional
in (2) realizes a minimization of the functional  . At the
. At the 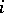 -th step of the process (2) the vector
-th step of the process (2) the vector 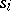 coincides with the direction of steepest descent (in gradient) of the surface
coincides with the direction of steepest descent (in gradient) of the surface  on the
on the 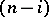 -dimensional ellipsoid formed by intersecting the surface with the plane conjugate to the directions
-dimensional ellipsoid formed by intersecting the surface with the plane conjugate to the directions  .
.
This method and its analogues have many different names, such as the Lanczos method, the Hestenes method, the Stiefel method, etc. Of all the methods for minimizing a functional, the conjugate-gradient method is best in strategic layout: it gives the maximal minimization after  steps. However, the calculations (2) under real conditions of machine arithmetic are sensitive to rounding-off errors, and the conditions (1) may be violated. This prevents termination of the process after
steps. However, the calculations (2) under real conditions of machine arithmetic are sensitive to rounding-off errors, and the conditions (1) may be violated. This prevents termination of the process after  steps. Therefore the method is continued beyond
steps. Therefore the method is continued beyond  iterations, and it can be regarded as an infinite iterative process for minimizing a functional. Modifications of the calculating scheme (2) that are more resistant to rounding-off errors are known (see [3], [4]).
iterations, and it can be regarded as an infinite iterative process for minimizing a functional. Modifications of the calculating scheme (2) that are more resistant to rounding-off errors are known (see [3], [4]).
References
| [1] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
| [2] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [3] | V.V. Voevodin, "Numerical methods of algebra" , Moscow (1966) (In Russian) |
| [4] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
The Stiefel method is related to the Zukhovitskii method for the minimax solution of a linear system, cf. [a1].
Modifications of the method of steepest descent can be found in [a1], [a12].
The classic reference for the conjugate-gradient method is [a4]. An up-to-date discussion with additional references is [a3]. Its relation with matrix factorization is discussed in [a9].
It appears that J.K. Reid was the first to use this method as an iterative method (cf. [a8]).
Several modifications have been proposed. E.g. the pre-conditioned conjugate-gradient method (cf. [a2]), and conjugate-gradient methods using incomplete Cholesky factorization (so-called ICCG methods, cf. [a7] and [a6]).
Extensions to non-symmetric conjugate-gradient methods are discussed in [a1] and [a10].
References
| [a1] | O. Axelsson, "Conjugate gradient type methods for unsymmetric and inconsistent systems of linear equations" Lin. Alg. and its Appl. , 34 (1980) pp. 1–66 |
| [a2] | P. Concus, G.H. Golub, D.P. O'Leary, "A generalized conjugate gradient method for the numerical solution of elliptic partial differential equations" J.R. Bunch (ed.) D.J. Rose (ed.) , Sparse matrix computations , Acad. Press (1976) |
| [a3] | G.H. Golub, C.F. van Loan, "Matrix computations" , North Oxford Acad. (1983) |
| [a4] | M.R. Hestenes, "Conjugate directions methods in optimization" , Springer (1980) |
| [a5] | M.R. Hestenes, E. Stiefel, "Methods of conjugate gradients for solving linear systems" J. Res. Nat. Bur. Stand. , 49 (1952) pp. 409–436 |
| [a6] | T.A. Manteuffel, "Shifted incomplete Cholesky factorization" I.S. Duff (ed.) G.W. Stewart (ed.) , Sparse matrix proceedings , SIAM Publ. (1979) |
| [a7] | J.A. Meijerink, H.A. van der Vorst, "An iterative solution method for linear systems of which the coefficient matrix is a symmetric 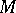 -matrix" Math. Comp. , 31 (1977) pp. 148–162 -matrix" Math. Comp. , 31 (1977) pp. 148–162 |
| [a8] | J.K. Reid, "On the method of conjugate gradients for the solution of large systems of linear equations" J.K. Reid (ed.) , Large sparse sets of linear equations , Acad. Press (1971) |
| [a9] | G.W. Stewart, "Conjugate gradients methods for solving systems of linear equations" Numerical Math. , 21 (1973) pp. 284–297 |
| [a10] | D.M. Young, K.C. Jea, "Generalized conjugate gradient acceleration of non-symmetrizable iterative methods" Lin. Alg. and its Appl. , 34 (1980) pp. 159–194 |
| [a11] | S.I. [S.I. Zukhovitskii] Zukhovitsky, L.I. Avdeeva, "Linear and convex programming" , Saunders (1966) |
| [a12] | G. Zoutendijk, "Methods of feasible directions" , Elsevier (1960) |
Conjugate gradients, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_gradients,_method_of&oldid=15751