Conjugate function
A concept in the theory of functions which is a concrete image of some involutory operator for the corresponding class of functions.
1) The function conjugate to a complex-valued function 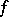 is the function
is the function  whose values are the complex conjugates of those of
whose values are the complex conjugates of those of  .
.
2) For the function conjugate to a harmonic function see Conjugate harmonic functions.
3) The function conjugate to a 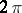 -periodic summable function
-periodic summable function 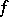 on
on 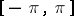 is given by
is given by
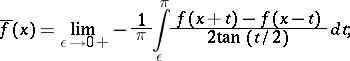 |
it exists almost-everywhere and coincides almost-everywhere with the  -sum,
-sum,  , and the Abel–Poisson sum of the conjugate trigonometric series.
, and the Abel–Poisson sum of the conjugate trigonometric series.
4) The function conjugate to a function 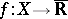 defined on a vector space
defined on a vector space 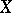 dual to a vector space
dual to a vector space  (with respect to a bilinear form
(with respect to a bilinear form 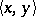 ) is the function on
) is the function on  given by
given by
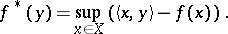 | (*) |
The conjugate of a function defined on  is defined in a similar way.
is defined in a similar way.
The function conjugate to the function 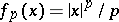 ,
,  , of one variable is given by
, of one variable is given by
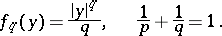 |
The function conjugate to the function 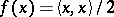 on a Hilbert space
on a Hilbert space 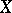 with scalar product
with scalar product 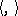 is the function
is the function 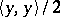 . The function conjugate to the norm
. The function conjugate to the norm 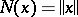 on a normed space is the function
on a normed space is the function 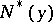 which is equal to zero when
which is equal to zero when 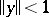 and to
and to 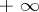 when
when 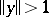 .
.
If 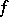 is smooth and increases at infinity faster than any linear function, then
is smooth and increases at infinity faster than any linear function, then 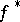 is just the Legendre transform of
is just the Legendre transform of 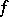 . For one-dimensional strictly-convex functions, a definition equivalent to (*) was given by W.H. Young [1] in other terms. He defined the conjugate of a function
. For one-dimensional strictly-convex functions, a definition equivalent to (*) was given by W.H. Young [1] in other terms. He defined the conjugate of a function
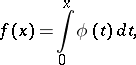 |
where 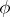 is continuous and strictly increasing, by the relation
is continuous and strictly increasing, by the relation
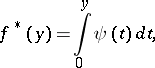 |
where 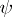 is the function inverse to
is the function inverse to 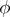 . Definition (*) was originally proposed by S. Mandelbrojt for one-dimensional functions, by W. Fenchel [2] in the finite-dimensional case, and by J. Moreau [3] and A. Brøndsted [4] in the infinite-dimensional case. For a convex function and its conjugate, Young's inequality holds:
. Definition (*) was originally proposed by S. Mandelbrojt for one-dimensional functions, by W. Fenchel [2] in the finite-dimensional case, and by J. Moreau [3] and A. Brøndsted [4] in the infinite-dimensional case. For a convex function and its conjugate, Young's inequality holds:
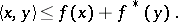 |
The conjugate function is a closed convex function. The conjugation operator 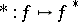 establishes a one-to-one correspondence between the family of proper closed convex functions on
establishes a one-to-one correspondence between the family of proper closed convex functions on  and that of proper closed convex functions on
and that of proper closed convex functions on  (the Fenchel–Moreau theorem).
(the Fenchel–Moreau theorem).
For more details see [5] and [6].
See also Convex analysis; Support function; Duality in extremal problems, Convex analysis; Dual functions.
References
| [1] | W.H. Young, "On classes of summable functions and their Fourier series" Proc. Roy. Soc. Ser. A. , 87 (1912) pp. 225–229 |
| [2] | W. Fenchel, "On conjugate convex functions" Canad. J. Math. , 1 (1949) pp. 73–77 |
| [3] | J.J. Moreau, "Fonctions convexes en dualité" , Univ. Montpellier (1962) |
| [4] | A. Brøndsted, "Conjugate convex functions in topological vector spaces" Math. Fys. Medd. Danske vid. Selsk. , 34 : 2 (1964) pp. 1–26 |
| [5] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) |
| [6] | V.M. Alekseev, V.M. Tikhomirov, S.V. Fomin, "Commande optimale" , MIR (1982) (Translated from Russian) |
Comments
The concepts of conjugate harmonic functions and conjugate trigonometric series are not unrelated. Let  be a harmonic function on the closed unit disc and
be a harmonic function on the closed unit disc and 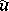 its harmonic conjugate, so that
its harmonic conjugate, so that 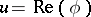 ,
, 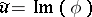 , where
, where 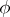 is the analytic function
is the analytic function 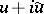 . Let
. Let  be the boundary value function of
be the boundary value function of  , i.e.
, i.e. 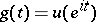 . Then one has the Poisson integral representation
. Then one has the Poisson integral representation
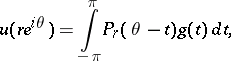 |
where
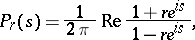 |
and
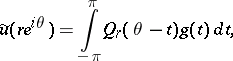 |
with
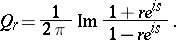 |
Then letting 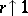 , (formally)
, (formally)
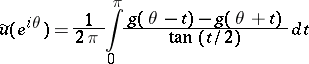 |
is precisely the conjugate trigonometric series of 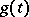 .
.
References
| [a1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1959) |
Conjugate function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_function&oldid=13183