Conjugate class of functions
A concept in the theory of functions which is a concrete instance of duality in functions spaces. Thus, if a class 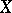 of functions is regarded as a Banach space or a topological vector space, then the conjugate class is defined as the class of functions isometrically isomorphic to the dual space
of functions is regarded as a Banach space or a topological vector space, then the conjugate class is defined as the class of functions isometrically isomorphic to the dual space 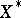 . For example, when
. For example, when 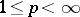 and
and 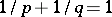 , there is an isometric isomorphism between the spaces
, there is an isometric isomorphism between the spaces 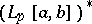 and
and 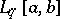 , under which corresponding elements
, under which corresponding elements 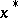 and
and 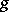 are related by
are related by
 |
If one considers some class 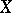 of
of 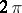 -periodic summable functions on
-periodic summable functions on 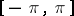 , then the conjugate class is defined to be the class of functions conjugate to the functions in
, then the conjugate class is defined to be the class of functions conjugate to the functions in 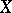 . For example, the class conjugate to
. For example, the class conjugate to 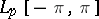 (
(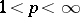 ) coincides with the class of functions
) coincides with the class of functions 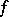 in
in  for which
for which
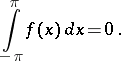 |
The class conjugate to  ,
, 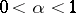 , coincides with the class of functions in
, coincides with the class of functions in 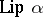 for which
for which 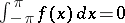 .
.
References
| [1] | M. Fréchet, C.R. Acad. Sci. , 144 (1907) pp. 1414–1416 |
| [2] | F. Riesz, C.R. Acad. Sci. , 144 (1907) pp. 1409–1411 |
| [3] | I. [I. Privalov] Priwaloff, Bull. Soc. Math. France , 44 (1916) pp. 100–103 |
| [4] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [5] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
Conjugate class of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_class_of_functions&oldid=12702