Congruence equation
algebraic congruence
A congruence of the form
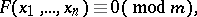 | (1) |
where
 |
is a polynomial in the variables  with integral rational coefficients
with integral rational coefficients 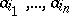 and
and 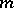 is an integer. The maximum value of the magnitude
is an integer. The maximum value of the magnitude
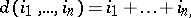 |
where the maximum is taken over all possible tuples 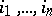 for which
for which 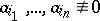 (
(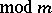 ), is called the degree with respect to the set of variables
), is called the degree with respect to the set of variables  or the degree of (1). The maximum value of the magnitudes
or the degree of (1). The maximum value of the magnitudes 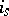 ,
, 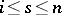 , where the maximum is taken over the same tuples
, where the maximum is taken over the same tuples 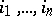 , is called the degree of the congruence equation with respect to the variable
, is called the degree of the congruence equation with respect to the variable 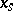 .
.
The principal problem in the theory of congruence equations is the number of solutions of a given congruence. It is possible to restrict the problem to the case of a prime module, since the problem of the number of solutions of (1) by a composite module 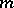 , except for a few degenerate cases, may be reduced to the problem of the number of solutions of the congruences
, except for a few degenerate cases, may be reduced to the problem of the number of solutions of the congruences 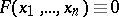 (
(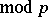 ) for the prime modules
) for the prime modules 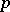 that are divisors of
that are divisors of 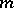 .
.
The most thoroughly studied congruence equations 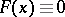 (
(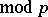 ) in one variable are the two-term congruences (cf. Two-term congruence)
) in one variable are the two-term congruences (cf. Two-term congruence)
 |
The study of the number of solutions of congruences in the case of a general polynomial  is very difficult, and only isolated partial solutions have so far been obtained.
is very difficult, and only isolated partial solutions have so far been obtained.
A system of congruences
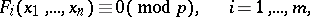 | (2) |
may be considered as a system of algebraic equations:
 |
over the finite prime field 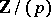 consisting of
consisting of  elements; the number of solutions of this system of congruences will be equal to the number of
elements; the number of solutions of this system of congruences will be equal to the number of 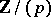 -rational points of the algebraic variety defined by the system of equations (2). Accordingly, together with number-theoretical methods, the methods of algebraic geometry are also used in the study of congruence equations or systems of such congruences.
-rational points of the algebraic variety defined by the system of equations (2). Accordingly, together with number-theoretical methods, the methods of algebraic geometry are also used in the study of congruence equations or systems of such congruences.
The most extensively studied congruence equations in several variables were those of the form
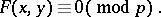 |
The estimate
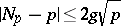 | (3) |
was obtained for the number of solutions 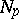 of a congruence of this type, where
of a congruence of this type, where 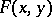 is an absolutely irreducible polynomial. The constant
is an absolutely irreducible polynomial. The constant 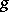 depends only on the polynomial and is equal to the genus of the curve
depends only on the polynomial and is equal to the genus of the curve 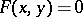 . Such an estimate for the first non-trivial case, viz. for the elliptic congruence
. Such an estimate for the first non-trivial case, viz. for the elliptic congruence
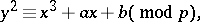 |
was obtained by H. Hasse in 1934, who based his work on the formula for the addition of points on the Jacobi variety of the curve 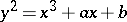 . Hasse's method was subsequently extended by A. Weil [4] to the case of absolutely irreducible polynomials
. Hasse's method was subsequently extended by A. Weil [4] to the case of absolutely irreducible polynomials 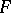 . This estimate was also obtained in [3] by elementary methods.
. This estimate was also obtained in [3] by elementary methods.
Studies of congruence equations with a number of variables 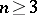 have been much less extensive. One general result is the theorem of Chevalley, according to which if
have been much less extensive. One general result is the theorem of Chevalley, according to which if 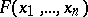 is a form the degree of which is strictly smaller than the number of variables, then the number of solutions of the congruence
is a form the degree of which is strictly smaller than the number of variables, then the number of solutions of the congruence
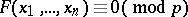 |
is positive and is divisible by 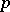 ; in the case of non-homogeneous polynomials the existence of a solution is not guaranteed, but the divisibility by
; in the case of non-homogeneous polynomials the existence of a solution is not guaranteed, but the divisibility by 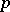 remains valid (Warning's theorem). This last theorem has been generalized to systems of congruences.
remains valid (Warning's theorem). This last theorem has been generalized to systems of congruences.
The theory of congruence equations has numerous applications in other branches of number theory — the theory of Diophantine equations, problems in additive number theory, algebraic number theory, etc.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian) |
| [3] | S.A. Stepanov, "A constructive method in the theory of equations over finite fields" Trudy Mat. Inst. Steklov. , 132 (1973) pp. 237–246 (In Russian) |
| [4] | A. Weil, "Courbes algébriques et variétés abéliennes. Sur les courbes algébriques et les varietés qui s'en deduisent" , Hermann (1948) |
Comments
A considerably more general result than (the generalization of) Warning's theorem was proved by P. Deligne (1973). He in fact proved the Riemann hypothesis for finite fields. This hypothesis, stated by Weil (1948), is closely connected with the zeta-function of (and the counting of points on) algebraic varieties over  . For Deligne's proof, see [a1] in the non-singular case and [a2] for the singular case. An overview of his result (and proofs) is in [a3]. For curves over finite fields the hard part of this Riemann hypothesis is the estimate (3). See [a4] for an easy proof of it. Estimates for the numbers of points on curves over
. For Deligne's proof, see [a1] in the non-singular case and [a2] for the singular case. An overview of his result (and proofs) is in [a3]. For curves over finite fields the hard part of this Riemann hypothesis is the estimate (3). See [a4] for an easy proof of it. Estimates for the numbers of points on curves over 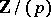 are also important in coding theory.
are also important in coding theory.
References
| [a1] | P. Deligne, "La conjecture de Weil, 1" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [a2] | P. Deligne, "La conjecture de Weil, 2" Publ. Math. IHES , 52 (1980) pp. 137–252 |
| [a3] | N.M. Katz, "An overview of Deligne's proof of the Riemann hypothesis for varieties over finite fields" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 275–305 |
| [a4] | E. Bombieri, "Counting points on curves over finite fields" Sém. Bourbaki , 430 (1972–1973) |
Congruence equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_equation&oldid=12343