Conformal Euclidean space

A Riemannian space admitting a conformal mapping onto a Euclidean space. The curvature tensor of a conformal Euclidean space has the form

(*)

where

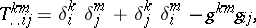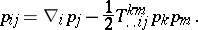For , every is a conformal Euclidean space. In order that a space with be a conformal Euclidean space, it is necessary and sufficient that there exist a tensor satisfying the conditions (*) and . Sometimes a conformal Euclidean space is called a Weyl space admitting a conformal mapping onto a Euclidean space (see [2]).

References

[1]	J.A. Schouten, D.J. Struik, "Einführung in die neueren Methoden der Differentialgeometrie" , 2 , Noordhoff (1935)
[2]	A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian)

Comments

The notion defined in the article above is also called a conformally Euclidean space. An alternative description of this notion is as follows. Let be an -dimensional Riemannian space with Riemannian metric 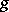, Levi-Civita derivation (cf. Levi-Civita connection) 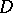, curvature tensor , Ricci transformation (cf. Ricci tensor) 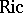, and scalar curvature . Then the conformal curvature tensor 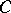(Weyl's curvature tensor) is defined by

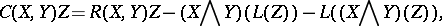where

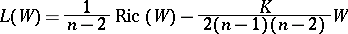and

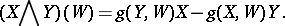Then locally admits a conformal mapping onto some open set of if and only if

1) for ; or

2) 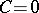and for .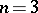

(See [a1] for example; for 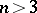the "Codazzi equationCodazzi equation" for 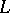is satisfied automatically.) The coordinate expressions for the equations given above can be found in the book of J.A. Schouten [a2].

References

[a1]	K. Yano, "The theory of Lie derivatives and its applications" , North-Holland (1957)
[a2]	J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) (Translated from German)