Confluent hypergeometric equation
degenerate hypergeometric equation
The second-order ordinary linear differential equation
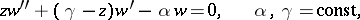 | (1) |
or, in self-adjoint form,
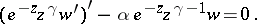 |
In general, the variables  and the parameters
and the parameters  may assume complex values. The Whittaker equation is a reduced form of equation (1). Equation (1) is closely connected with the hypergeometric equation. The confluent hypergeometric equation can be regarded as an equation obtained from the Riemann differential equation as a result of the merging of two singular points. The point
may assume complex values. The Whittaker equation is a reduced form of equation (1). Equation (1) is closely connected with the hypergeometric equation. The confluent hypergeometric equation can be regarded as an equation obtained from the Riemann differential equation as a result of the merging of two singular points. The point 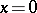 is a regular singular point for equation (1), while the point
is a regular singular point for equation (1), while the point  is a strong singular point (cf. Singular point). E.E. Kummer [1] was the first to undertake a systematic study of the solutions of equation (1).
is a strong singular point (cf. Singular point). E.E. Kummer [1] was the first to undertake a systematic study of the solutions of equation (1).
The solutions of equation (1) are expressed through the confluent hypergeometric function  . If
. If  is not an integer, the general solution of equation (1) may be written in the form
is not an integer, the general solution of equation (1) may be written in the form
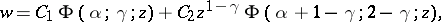 | (2) |
where  and
and 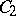 are arbitrary constants. This representation is valid in the complex
are arbitrary constants. This representation is valid in the complex  -plane with the slit
-plane with the slit 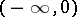 . If
. If 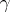 is an integer, the general solution has a more complicated form (may contain logarithmic terms). Functions other than those in (2) (e.g. Whittaker functions [2], [3]) can also be selected as a fundamental system of solutions of equation (1). Solutions of (1) can also be represented by contour integrals in the complex
is an integer, the general solution has a more complicated form (may contain logarithmic terms). Functions other than those in (2) (e.g. Whittaker functions [2], [3]) can also be selected as a fundamental system of solutions of equation (1). Solutions of (1) can also be represented by contour integrals in the complex  -plane.
-plane.
Many second-order ordinary linear differential equations (e.g. the Bessel equation) can be reduced to equation (1) by a transformation of the unknown function and of the independent variable [4]. In particular, equations of the type
 |
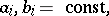 |
can be integrated using the confluent hypergeometric function.
References
| [1] | E.E. Kummer, "Ueber die hypergeometrische Reihe 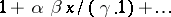 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
| [2] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [3] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [4] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
Confluent hypergeometric equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Confluent_hypergeometric_equation&oldid=13279