Cone condition

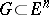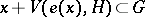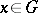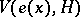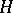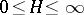A condition on a region of Euclidean space expressing some non-flatness property. An open set satisfies the weak cone condition if for all , where is a right circular cone with vertex at the origin of fixed opening and height , , and with axis vector 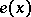depending on . An open set 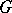satisfies the strong cone condition if there exists a covering of the closure 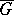by open sets 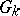such that for any 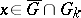the cone 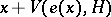is contained in 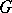(the openings of these cones may depend on 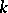). In connection with integral representations of functions and imbedding theorems, anisotropic generalizations of cone conditions have been considered, for example, the weak and strong 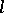-horn conditions (see [1]), the cube condition, etc.

References

[1]	O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , Wiley (1978) (Translated from Russian)

References

[a1]	S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965)