Conductor of a character
An integer associated to the character of a representation of the Galois group of a finite extension of a local field. Let 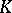 be a field that is complete with respect to a discrete valuation, with residue class field
be a field that is complete with respect to a discrete valuation, with residue class field 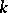 of characteristic
of characteristic 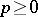 . Let
. Let 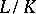 be a Galois extension of degree
be a Galois extension of degree  with Galois group
with Galois group 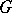 and suppose that the residue class field extension is separable. If
and suppose that the residue class field extension is separable. If 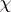 is the character of some finite-dimensional complex representation of
is the character of some finite-dimensional complex representation of 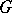 , its conductor
, its conductor 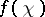 is defined by the formula:
is defined by the formula:
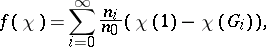 |
where
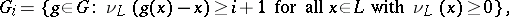 |
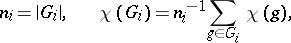 |
where 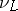 is the corresponding valuation of
is the corresponding valuation of 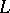 . If
. If 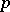 does not divide
does not divide  , then
, then 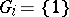 for
for 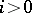 and
and 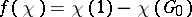 . If
. If 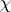 is the character of a rational representation
is the character of a rational representation 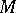 , then
, then 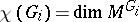 . The conductor
. The conductor 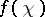 is a non-negative integer.
is a non-negative integer.
References
| [1] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) pp. Chapt. VI |
| [2] | E. Artin, J. Tate, "Class field theory" , Benjamin (1967) |
| [3] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) |
Comments
The ideal 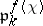 , where
, where 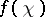 is the conductor of a character
is the conductor of a character 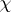 of the Galois group of an extension of local fields, is also called the Artin conductor of
of the Galois group of an extension of local fields, is also called the Artin conductor of 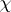 . There is a corresponding notion for extensions of global fields obtained by taking a suitable product over all finite primes, cf. [a1], p. 126. It plays an important role in the theory of Artin
. There is a corresponding notion for extensions of global fields obtained by taking a suitable product over all finite primes, cf. [a1], p. 126. It plays an important role in the theory of Artin 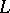 -functions, cf.
-functions, cf. 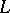 -function.
-function.
References
| [a1] | J. Neukirch, "Class field theory" , Springer (1986) |
Conductor of a character. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conductor_of_a_character&oldid=19015