Concentration function
of a random variable 
The function  defined for all non-negative
defined for all non-negative  and random variables
and random variables  by the formula
by the formula
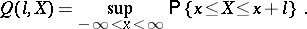 |
The concentration function  is a non-negative, semi-additive, monotone decreasing function for
is a non-negative, semi-additive, monotone decreasing function for  , right continuous and such that
, right continuous and such that
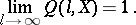 |
Conversely, any function possessing these properties can be regarded as the concentration function of some random variable.
The concentration function is a convenient characterization of the scatter of the values of a random variable, especially for the quantitative expression of the increase of the scatter under summation of independent random variables. The first absolute (that is, containing only absolute constants) estimate for the concentration of the sum under given concentrations of the components was obtained by A.N. Kolmogorov [4] by developing a method due to P. Lévy [2]. This result was subsequently strengthened (see ). The following statement was obtained, which includes all earlier results as special cases:
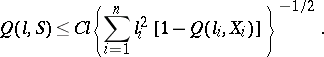 |
Here
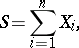 |
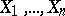 is a set of independent random variables,
is a set of independent random variables, 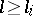 ,
, 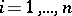 , and
, and  is an absolute constant. Two types of estimates are singled out: estimates of
is an absolute constant. Two types of estimates are singled out: estimates of 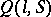 of local type (see [6]), and estimates of
of local type (see [6]), and estimates of 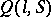 of integral type (see [7]).
of integral type (see [7]).
A dual characterization of the scatter, closely related to the concentration function, is the scattering function of the random variable 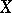 :
:
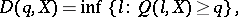 |
where 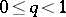 . There is (see [8]) the following inequality relating the concentration function and the characteristic function
. There is (see [8]) the following inequality relating the concentration function and the characteristic function 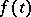 of a random variable
of a random variable 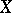 :
:
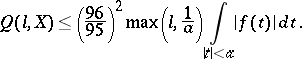 |
The inequalities
 |
where 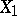 and
and 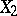 are independent random variables, also hold. There have been attempts to carry over certain results touching upon concentration functions to the case of summation of independent random vectors (see [9]).
are independent random variables, also hold. There have been attempts to carry over certain results touching upon concentration functions to the case of summation of independent random vectors (see [9]).
References
| [1] | W. Doeblin, P. Lévy, "Calcul des probabilités. Sur les sommes de variables aléatoires indépendantes à dispersions bornées inférieurement" C.R. Acad. Sci. , 202 (1936) pp. 2027–2029 |
| [2] | P. Lévy, "Théorie de l'addition des variables aléatoires" , Gauthier-Villars (1937) |
| [3] | W. Doeblin, "Sur les sommes d'un grand nombre de variables aléatoires indépendantes" Bull. Sci. Math. , 63 (1939) pp. 23–64 |
| [4] | A. Kolmogorov, "Sur les propriétés des fonctions de concentration de M. P. Lévy" Ann. Inst. H. Poincaré , 16 (1958–1960) pp. 27–34 |
| [5a] | B.A. Rogozin, "An estimate for concentration functions" Theory Probab. Appl. , 6 (1961) pp. 94–96 Teoriya Veroyatnost. i Prilozhen. , 6 (1961) pp. 103–105 |
| [5b] | B.A. Rogozin, "On the increase of dispersion of sums of independent random variables" Theory Probab. Appl. , 6 (1961) pp. 97–99 Teoriya Veroyatnost. i Prilozhen. , 6 (1961) pp. 106–108 |
| [6] | H. Kesten, "A sharper form of the Doeblin–Lévy–Kolmogorov–Rogozin inequality for concentration functions" Math. Scand. , 25 (1969) pp. 133–144 |
| [7] | B.A. Rogozin, "An integral-type estimate for concentration functions of sums of independent random variables" Dokl. Akad. Nauk SSSR , 211 (1973) pp. 1067–1070 (In Russian) |
| [8] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [9] | C.G. Esseen, "On the concentration function of a sum of independent random variables" Z. Wahrscheinlichkeitstheor. und Verw. Geb. , 9 (1968) pp. 290–308 |
Concentration function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Concentration_function&oldid=11867