Difference between revisions of "Computational complexity classes"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 190 formulas, 182 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
Computational complexity measures the amount of computational resources, such as time and space, that are needed to compute a function. | Computational complexity measures the amount of computational resources, such as time and space, that are needed to compute a function. | ||
| − | In the 1930s many models of computation were invented, including Church's | + | In the 1930s many models of computation were invented, including Church's $\lambda$-calculus (cf. [[Lambda-calculus|$\lambda$-calculus]]), Gödel's recursive functions, Markov algorithms (cf. also [[Algorithm|Algorithm]]) and Turing machines (cf. also [[Turing machine|Turing machine]]). All of these independent efforts to precisely define the intuitive notion of "mechanical procedure" were proved equivalent. This led to the universally accepted Church thesis, which states that the intuitive concept of what can be "automatically computed" is appropriately captured by the Turing machine (and all its variants); cf. also [[Church thesis|Church thesis]]; [[Computable function|Computable function]]. |
| − | Computational complexity studies the inherent difficulty of computational problems. Attention is confined to decision problems, i.e., sets of binary strings, | + | Computational complexity studies the inherent difficulty of computational problems. Attention is confined to decision problems, i.e., sets of binary strings, $S \subseteq \Sigma ^ {\color{blue} * }$, where $\Sigma = \{ 0,1 \}$. In a decision problem $S$ the input binary string $w$ is accepted if $w \in S$ and rejected if $w \notin S$ (cf. also [[Decision problem|Decision problem]]). |
| − | For any function | + | For any function $t ( n )$ from the positive integers to itself, the complexity class $\operatorname {DTIME}[t(n)]$ is the set of decision problems that are computable by a deterministic, multi-tape Turing machine in $O ( t ( n ) )$ steps for inputs of length $n$. |
| − | Polynomial time ( | + | Polynomial time ($P$) is the set of decision problems accepted by Turing machines using at most some polynomial number of steps, $P = \cup _ { k = 1 } ^ { \infty } \operatorname { DTIME } [ n ^ { k } ] = \operatorname { DTIME } [ n ^ { O ( 1 ) } ]$. |
| − | Intuitively, a decision problem is "feasible" if it can be computed with an "affordable" amount of time and hardware, on all "reasonably sized" instances. | + | Intuitively, a decision problem is "feasible" if it can be computed with an "affordable" amount of time and hardware, on all "reasonably sized" instances. $P$ is a mathematically elegant and useful approximation to the set of feasible problems. Most natural problems that are in $P$ have small exponents and multiplicative constants in their running time and thus are also feasible. This includes sorting, inverting matrices, pattern matching, linear programming, network flow, graph connectivity, shortest paths, minimal spanning trees, strongly connected components, testing planarity, and convex hull. |
| − | The complexity class | + | The complexity class $\operatorname{NTIME} [t( n )]$ is the set of decision problems that are accepted by a non-deterministic multi-tape Turing machine in $O ( t ( n ) )$ steps for inputs of length $n$. A non-deterministic Turning machine may make one of several possible moves at each step. One says that it "accepts an input" if at least one of its possible computations on that input is accepting. The time is the maximum number of steps that any computation may take on this input, not the exponentially greater number of steps required to simulate all possible computations on that input. |
| − | Non-deterministic polynomial time ( | + | Non-deterministic polynomial time ($\operatorname{NP}$) is the set of decision problems accepted by a non-deterministic Turing machine in some polynomial time, $\operatorname { NP} = \operatorname { NTIME} [ n ^ { O ( 1 ) } ]$. For example, let $\operatorname{SAT}$ be the set of Boolean formulas that have some assignment of their Boolean variables making them true (cf. also [[Boolean algebra|Boolean algebra]]). The formula $\phi \equiv ( x _ { 1 } \vee x _ { 2 } ) \wedge ( \overline { x _ { 2 } } \vee \overline { x _ { 3 } } ) \wedge ( \overline { x _ { 1 } } \vee x _ { 3 } )$ is in $\operatorname{SAT}$ because the assignment that makes $x_{1} $ and $x _ { 3 }$ true and $x _ { 2 }$ false satisfies $\phi$. Given a formula with $k$ Boolean variables, a non-deterministic machine can non-deterministically write a binary string of length $k$ and then check if the assignment it has written down satisfies the formula, accepting if it does. Thus $\operatorname{SAT} \in \operatorname{NP}$. The decision versions of many important optimization problems, including travelling salesperson, graph colouring, clique, knapsack, bin packing and processor scheduling, are in $\operatorname{NP}$. |
| − | The complexity class | + | The complexity class $\operatorname{DSPACE}[s(n)]$ is the set of decision problems that are accepted by a deterministic Turing machine that uses at most $O ( t ( n ) )$ tape cells for inputs of length $n$. It is assumed that the input tape is read-only and space is only charged for the other tapes. Thus it makes sense to talk about space less than $n$. |
| − | Similarly one defines the non-deterministic space classes, | + | Similarly one defines the non-deterministic space classes, $\operatorname{NSPACE}[s(n)]$. On inputs of length $n$, an $\operatorname{NSPACE}[s(n)]$ Turing machine uses at most $O ( s ( n ) )$ tape cells on each of its computations. One says it "accepts an input" if at least one of its computations on that input is accepting. The main space complexity classes are polynomial space, $\operatorname { PSPACE }= \operatorname { DSPACE } [ n ^ { O ( 1 ) } ]$; Logspace, $L = \operatorname{DSPACE} [\operatorname{log} n]$; and non-deterministic logspace, $\operatorname{NL} = \operatorname{NSPACE} [ \operatorname { log } n ]$. |
For each of the above resources (deterministic and non-deterministic time and space) there is a hierarchy theorem saying that more of the given resource enables one to compute more decision problems. These theorems are proved by diagonalization arguments: use the greater amount of the resource to simulate all machines using the smaller amount, and do something different from the simulated machine in each case. | For each of the above resources (deterministic and non-deterministic time and space) there is a hierarchy theorem saying that more of the given resource enables one to compute more decision problems. These theorems are proved by diagonalization arguments: use the greater amount of the resource to simulate all machines using the smaller amount, and do something different from the simulated machine in each case. | ||
==Hierarchy theorems.== | ==Hierarchy theorems.== | ||
| − | See also [[#References|[a11]]], [[#References|[a10]]], [[#References|[a4]]], [[#References|[a20]]]. In the statement of these theorems the notion of a space- or time-constructible function is used. Recall that a function | + | See also [[#References|[a11]]], [[#References|[a10]]], [[#References|[a4]]], [[#References|[a20]]]. In the statement of these theorems the notion of a space- or time-constructible function is used. Recall that a function $s$ from the positive integers to itself is space constructible (respectively, time constructible) if and only if there is a deterministic Turing machine running in space $O ( s ( n ) )$ (respectively, time $O ( s ( n ) )$) that on every input of length $n$ computes the number $s ( n )$ in binary. Every reasonable function is constructible. |
The following are hierarchy theorems: | The following are hierarchy theorems: | ||
| − | 1) For all space constructible | + | 1) For all space constructible $s ( n ) \geq \operatorname { log } n$, if |
| − | + | \begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { t ( n ) } { s ( n ) } = 0, \end{equation*} | |
| − | then | + | then $\operatorname{DSPACE}[t(n)]$ is strictly contained in $\operatorname{DSPACE}[s(n)]$, and $\text{NSPACE} [t( n )]$ is strictly contained in $\operatorname{NSPACE}[s(n)]$. |
| − | 2) For all time constructible | + | 2) For all time constructible $t ( n ) \geq n$, if |
| − | + | \begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { t ( n ) } { s ( n ) } = 0, \end{equation*} | |
| − | then | + | then $\operatorname{NTIME} [t( n )]$ is strictly contained in $\text{NTIME} \, [ s ( n ) ]$. |
| − | 3) For all time constructible | + | 3) For all time constructible $t ( n ) \geq n$, if |
| − | + | \begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } t ( n ) ( \operatorname { log } t ( n ) ) / s ( n ) = 0, \end{equation*} | |
| − | then | + | then $\operatorname {DTIME}[t(n)]$ is strictly contained in $\operatorname{DTIME}[ s ( n ) ]$ |
| − | The slightly stronger requirement in the last of the above theorems has to do with the extra factor of time | + | The slightly stronger requirement in the last of the above theorems has to do with the extra factor of time $\operatorname{log} ( t ( n ) )$ that is required for a two-tape Turing machine to simulate a machine with more than two tapes. If one restricts attention to multi-tape Turing machines with a fixed number of tapes, then a strict hierarchy theorem for deterministic time results [[#References|[a8]]]. |
| − | Much less is know when comparing different resources: One can simulate | + | Much less is know when comparing different resources: One can simulate $\operatorname{NTIME} [t( n )]$ in $\operatorname{DSPACE}[t(n)]$ by simulating all the non-deterministic computations in turn. One can simulate $\operatorname{DSPACE}[s(n)]$ in $\operatorname{DTIME}[ 2 ^ { O ( s ( n ) ) } ]$ because a $\operatorname{DSPACE}[s(n)]$ computation can be in one of at most $2 ^ { O ( s ( n ) ) }$ possible configurations. |
| − | Savitch's theorem provides a non-trivial relationship between deterministic and non-deterministic space [[#References|[a19]]]: For | + | Savitch's theorem provides a non-trivial relationship between deterministic and non-deterministic space [[#References|[a19]]]: For $s ( n ) \geq \operatorname { log } n$, |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c13016072.png"/></td> </tr></table> |
| − | For each decision problem | + | For each decision problem $S \subseteq \Sigma ^ {\color{blue} * }$, its complement $\bar{S} = \Sigma ^ {\color{blue} * } - S$ is also a decision problem. For each complexity class $\mathcal{C}$, define its complementary class by |
| − | + | \begin{equation*} \operatorname { co } \mathcal{C} = \{ S : \overline{S} \in \mathcal{C} \}. \end{equation*} | |
| − | For deterministic classes | + | For deterministic classes $\mathcal{C}$, such as $P$, $L$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c13016080.png"/>, it is obvious that ${\cal C} = \operatorname { co }\cal C$. However, this is much less clear for non-deterministic classes. Since the definitions of $\text{NTIME}$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c13016083.png"/> were made, it was widely believed that $\text{NP} \neq \operatorname{co} \text{NP}$ and $\text{NSPACE }[ n ] \neq\text{co NSPACE }[n]$. However, in 1987 the latter was shown to be false [[#References|[a25]]], [[#References|[a18]]]. In fact, the following Immerman–Szelepcsényi theorem holds: For $s ( n ) \geq \operatorname { log } n$, $\text{NSPACE} [ s ( n ) ] = \text { co } \text{NSPACE} [ s ( n ) ]$. |
| − | Even though complexity classes are all defined as sets of decision problems, one can define functions computable in a complexity class as follows. For a complexity class | + | Even though complexity classes are all defined as sets of decision problems, one can define functions computable in a complexity class as follows. For a complexity class $\mathcal{C}$, define $F ( {\cal C} )$ to be the set of all polynomially-bounded functions $f : \Sigma ^ { \color{blue}* } \rightarrow \Sigma ^ { \color{blue} * }$ such that each bit of $f$ (thought of as a decision problem) is in $\mathcal{C}$ and $\text{co} \mathcal{C}$. |
| − | One compares the complexity of decision problems by reducing one to the other as follows. Let | + | One compares the complexity of decision problems by reducing one to the other as follows. Let $A , B \subseteq \Sigma ^ { * }$. $A$ is reducible to $B$ ($A \leq B$) if and only if there exists a function $f \in F ( L )$ such that for all $w \in \Sigma ^ {\color{blue} * }$, $w \in A$ if and only if $f ( w ) \in B$. The question whether $w$ is a member of $A$ is thus reduced to the question of whether $f ( w )$ is a member of $B$. If $f ( w ) \in B$, then $w \in A$. Conversely, if $f ( w ) \notin B$, then $w \notin A$. |
| − | The complexity classes, i.e., | + | The complexity classes, i.e., $L$, $\operatorname{NL}$, $P$, $\operatorname{NP}$, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c130160114.png"/>, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c130160115.png"/>, are all closed under reductions in the following sense: If $\mathcal{C}$ is one of the above classes, $A \leq B$, and $B \in \mathcal{C}$, then $A \in \mathcal{C}$. |
| − | A problem | + | A problem $A$ is complete for complexity class $\mathcal{C}$ if and only if $A \in \mathcal{C}$ and for all $B \in \mathcal{C}$, $B < A$. If $\mathcal{C}$ is closed under reductions, then any complete problem, say $A$, characterizes the complexity class, because for all $B$, $B \in \mathcal{C}$ implies $B < A$. |
| − | Most natural complexity classes include a large number of interesting complete problems. See [[#References|[a9]]], [[#References|[a15]]], [[#References|[a14]]] for substantial collections of problems that are complete for | + | Most natural complexity classes include a large number of interesting complete problems. See [[#References|[a9]]], [[#References|[a15]]], [[#References|[a14]]] for substantial collections of problems that are complete for $\operatorname{NP}$, $P$, and $\operatorname{NL}$, respectively. |
| − | A non-deterministic machine can be thought of as a parallel machine with weak communication. At each step, each processor | + | A non-deterministic machine can be thought of as a parallel machine with weak communication. At each step, each processor $p$ may create copies of itself and set them to work on slightly different problems. If any of these offspring ever reports acceptance to $p$, then $p$ in turn reports acceptance to its parent. Each processor thus reports the "or" of its children. |
| − | A. Chandra, D.C. Kozen and L. Stockmeyer generalized non-deterministic Turing machines to alternating Turing machines, in which there are "or" states, reporting the "or" of their children, and there are "and" states, reporting the "and" of their children. They proved the following alternation theorem [[#References|[a3]]]: For | + | A. Chandra, D.C. Kozen and L. Stockmeyer generalized non-deterministic Turing machines to alternating Turing machines, in which there are "or" states, reporting the "or" of their children, and there are "and" states, reporting the "and" of their children. They proved the following alternation theorem [[#References|[a3]]]: For $s ( n ) \geq \operatorname { log } n$ and $t ( n ) \geq n$, |
| − | + | \begin{equation*} \operatorname {ATIME}[ ( t ( n ) ) ^ { O ( 1 ) } ] = \operatorname { DSPACE } [ ( t ( n ) ) ^ { O ( 1 ) } ]; \end{equation*} | |
| − | + | \begin{equation*} \operatorname { ASPACE } [ s ( n ) ] = \operatorname { DTIME } [ 2 ^ { O ( s ( n ) ) } ]. \end{equation*} | |
| − | In particular, | + | In particular, $\operatorname{ASPACE}[\operatorname{log} n] = P$ and $\operatorname{ATIME} [ n ^ { O ( 1 ) } ] = \operatorname { PSPACE }$. |
| − | Let the class | + | Let the class $\text{ASPACETIME} \, [ s ( n ) , t ( n ) ]$ (respectively, $\text{ATIMEALT} [ t ( n ) , a ( n )]$) be the set of decision problems accepted by alternating machines simultaneously using space $s ( n )$ and time $t ( n )$ (respectively, time $t ( n )$ and making at most $a ( n )$ alternations between existential and universal states, and starting with existential). Thus $\operatorname{ATIMEALT}[ n ^ { O ( 1 ) } , 1 ] = \operatorname{NP}$. The polynomial-time hierarchy ($\operatorname{PH}$) is the set of decision problems accepted in polynomial time by alternating Turing machines making a bounded number of alternations between existential and universal states, $\operatorname{PH} = \operatorname{ATIMEALT} [ n ^ { O ( 1 ) } , O ( 1 ) ]$. |
| − | + | $\text{NC}$ is the set of decision problems recognizable by a [[Parallel random access machine|parallel random access machine]] (a PRAM) using polynomially much hardware and parallel time $( \operatorname { log } n ) ^ { O ( 1 ) }$. $\text{NC}$ is often studied using uniform classes of acyclic circuits of polynomial size and depth $( \operatorname { log } n ) ^ { O ( 1 ) }$. $\text{NC}$ is characterized via alternating complexity in the following way, | |
| − | + | \begin{equation*} \operatorname{NC} = \text { ASPACETIME } [ \operatorname { log } n , ( \operatorname { log } n ) ^ { O ( 1 ) } ]. \end{equation*} | |
| − | A decision problem is complex if and only if it has a complex description. This leads to a characterization of complexity via logic. The input object, e.g., a string or a graph, is thought of as a (finite) logical structure. R. Fagin characterized | + | A decision problem is complex if and only if it has a complex description. This leads to a characterization of complexity via logic. The input object, e.g., a string or a graph, is thought of as a (finite) logical structure. R. Fagin characterized $\operatorname{NP}$ as the set of second-order expressible properties ($\operatorname{NP} = \operatorname{SO} ( \exists )$), N. Immerman and M.Y. Vardi characterized $P$ as the set of properties expressible in first-order logic plus a least-fixed-point operator ($P = \operatorname{FO} ( \operatorname{LFP} )$). In fact, all natural complexity classes have natural descriptive characterizations [[#References|[a7]]], [[#References|[a24]]], [[#References|[a22]]], [[#References|[a5]]], [[#References|[a23]]]. |
| − | A probabilistic Turing machine is one that may flip a series of fair coins as part of its computation. A decision problem | + | A probabilistic Turing machine is one that may flip a series of fair coins as part of its computation. A decision problem $S$ is in bounded probabilistic polynomial time ($\operatorname {BPP}$) if and only if there is a probabilistic polynomial-time Turing machine $M$ such that for all inputs $w$, if $( w \in S )$, then $\mathsf{P}(M \ \text{accepts} \ w) \geq 2 / 3$, and if $( w \notin S )$, then $P(M\, \text{accepts}\, w)\leq 1 / 3$. |
| − | It follows by running | + | It follows by running $M ( w )$ polynomially many times that the probability of error can be made at most $2 ^ { - n ^ { k } }$ for any fixed $k$ and inputs of length $n$. It is believed that $P = \operatorname {BPP}$. An important problem in $\operatorname {BPP}$ that is not known to be in $P$ is primality, [[#References|[a21]]]. |
| − | Recent work (1998) on randomness and cryptography has led to a new and surprising characterization of | + | Recent work (1998) on randomness and cryptography has led to a new and surprising characterization of $\operatorname{NP}$ via interactive proofs [[#References|[a1]]]. This in turn has led to tight bounds on how closely many $\operatorname{NP}$ optimization problems can be approximated in polynomial time, assuming that $P \neq \text{NP}$ [[#References|[a13]]]. |
| − | It is known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c130160179.png" />, so by the space hierarchy theorem | + | It is known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c130160179.png"/>, so by the space hierarchy theorem $\text{NC}$ (and thus of course $\operatorname{NL}$ and $L$) is strictly contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130160/c130160183.png"/>. Strong lower bounds have been proved on some circuit complexity classes below $L$ [[#References|[a2]]], [[#References|[a6]]], [[#References|[a12]]], [[#References|[a17]]]; but even now (2001), thirty years after the introduction of the classes $P$ and $\operatorname{NP}$, no other inequality concerning the following containments, including that $L$ is not equal to $\operatorname{PH}$, is known: |
| − | + | \begin{equation*} L \subseteq \operatorname{NL} \subseteq \operatorname{NC} \subseteq P \subseteq \operatorname{NP} \subseteq \operatorname{PH} \subseteq \operatorname{PSPACE}. \end{equation*} | |
For further reading, an excellent textbook on computational complexity is [[#References|[a16]]]. | For further reading, an excellent textbook on computational complexity is [[#References|[a16]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> S. Arora, C. Lund, R. Motwani, M. Sudan, M. Szegedy, "Proof verification and the hardness of approximation problems" ''J. Assoc. Comput. Mach.'' , '''45''' : 3 (1998) pp. 501–555</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Ajtai, "$\Sigma ^ { 1 _ { 1 }}$ formulae on finite structures" ''Ann. Pure Appl. Logic'' , '''24''' (1983) pp. 1–48</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Chandra, L. Stockmeyer, "Alternation" , ''Proc. 17th IEEE Symp. Found. Computer Sci.'' (1976) pp. 151–158</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> S.A. Cook, "A hierarchy for nondeterministic time complexity" ''J. Comput. Syst. Sci.'' , '''7''' : 4 (1973) pp. 343–353</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H.-D. Ebbinghaus, J. Flum, "Finite model theory" , Springer (1995)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M. Furst, J.B. Saxe, M. Sipser, "Parity, circuits, and the polynomial-time hierarchy" ''Math. Systems Th.'' , '''17''' (1984) pp. 13–27</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> R. Fagin, "Generalized first-order spectra and polynomial-time recognizable sets" R. Karp (ed.) , ''Complexity of Computation (SIAM-AMS Proc.)'' , '''7''' , Amer. Math. Soc. (1974) pp. 27–41</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> M. Fürer, "The tight deterministic time hierarchy" , ''14th ACM STOC Symp.'' (1982) pp. 8–16</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> M.R. Garey, D.S. Johnson, "Computers and intractability" , Freeman (1979)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J. Hartmanis, P.M. Lewis, R.E. Stearns, "Hierarchies of memory limited computations" , ''Sixth Ann. IEEE Symp. Switching Circuit Theory and Logical Design'' (1965) pp. 179–190</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> J. Hartmanis, R. Stearns, "On the computational complexity of algorithms" ''Trans. Amer. Math. Soc.'' , '''117''' : 5 (1965) pp. 285–306</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> J. Hastad, "Almost optimal lower bounds for small depth circuits" , ''18th ACM STOC Symp.'' (1986) pp. 6–20</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> "Approximation algorithms for NP hard problems" D. Hochbaum (ed.) , PWS (1997)</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> N. Jones, E. Lien, W. Laaser, "New problems complete for nondeterministic logspace" ''Math. Systems Th.'' , '''10''' (1976) pp. 1–17</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> R. Greenlaw, H.J. Hoover, L. Ruzzo, "Limits to parallel computation: P-completeness theory" , Oxford Univ. Press (1995)</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> C.H. Papadimitriou, "Complexity" , Addison-Wesley (1994)</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> A.A. Razborov, "Lower bounds on the size of bounded depth networks over a complete basis with logical addition" ''Math. Notes'' , '''41''' (1987) pp. 333–338 ''Mat. Zametki'' , '''41''' (1987) pp. 598–607</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> R. Szelepcsényi, "The method of forced enumeration for nondeterministic automata" ''Acta Inform.'' , '''26''' (1988) pp. 279–284</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> W. Savitch, "Relationships between nondeterministic and deterministic tape complexities" ''J. Comput. Syst. Sci.'' , '''4''' (1970) pp. 177–192</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> J.I. Seiferas, M.J. Fischer, A.R. Meyer, "Refinements of nondeterministic time an space hierarchies" , ''Proc. Fourteenth Ann. IEEE Symp. Switching and Automata Theory'' (1973) pp. 130–137</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> R. Solovay, V. Strassen, "A fast Monte-Carlo test for primality" ''SIAM J. Comput.'' , '''6''' (1977) pp. 84–86</td></tr><tr><td valign="top">[a22]</td> <td valign="top"> M.Y. Vardi, "Complexity of relational query languages" , ''14th Symp. Theory of Computation'' (1982) pp. 137–146</td></tr><tr><td valign="top">[a23]</td> <td valign="top"> N. Immerman, "Descriptive complexity" , ''Graduate Texts in Computer Sci.'' , Springer (1999)</td></tr><tr><td valign="top">[a24]</td> <td valign="top"> N. Immerman, "Relational queries computable in polynomial time" , ''14th ACM STOC Symp.'' (1982) pp. 147–152 (Revised version: Inform. & Control 68 (1986), 86-104)</td></tr><tr><td valign="top">[a25]</td> <td valign="top"> N. Immerman, "Nondeterministic space is closed under complementation" ''SIAM J. Comput.'' , '''17''' : 5 (1988) pp. 935–938</td></tr></table> |
Latest revision as of 17:43, 1 July 2020
Computational complexity measures the amount of computational resources, such as time and space, that are needed to compute a function.
In the 1930s many models of computation were invented, including Church's $\lambda$-calculus (cf. $\lambda$-calculus), Gödel's recursive functions, Markov algorithms (cf. also Algorithm) and Turing machines (cf. also Turing machine). All of these independent efforts to precisely define the intuitive notion of "mechanical procedure" were proved equivalent. This led to the universally accepted Church thesis, which states that the intuitive concept of what can be "automatically computed" is appropriately captured by the Turing machine (and all its variants); cf. also Church thesis; Computable function.
Computational complexity studies the inherent difficulty of computational problems. Attention is confined to decision problems, i.e., sets of binary strings, $S \subseteq \Sigma ^ {\color{blue} * }$, where $\Sigma = \{ 0,1 \}$. In a decision problem $S$ the input binary string $w$ is accepted if $w \in S$ and rejected if $w \notin S$ (cf. also Decision problem).
For any function $t ( n )$ from the positive integers to itself, the complexity class $\operatorname {DTIME}[t(n)]$ is the set of decision problems that are computable by a deterministic, multi-tape Turing machine in $O ( t ( n ) )$ steps for inputs of length $n$.
Polynomial time ($P$) is the set of decision problems accepted by Turing machines using at most some polynomial number of steps, $P = \cup _ { k = 1 } ^ { \infty } \operatorname { DTIME } [ n ^ { k } ] = \operatorname { DTIME } [ n ^ { O ( 1 ) } ]$.
Intuitively, a decision problem is "feasible" if it can be computed with an "affordable" amount of time and hardware, on all "reasonably sized" instances. $P$ is a mathematically elegant and useful approximation to the set of feasible problems. Most natural problems that are in $P$ have small exponents and multiplicative constants in their running time and thus are also feasible. This includes sorting, inverting matrices, pattern matching, linear programming, network flow, graph connectivity, shortest paths, minimal spanning trees, strongly connected components, testing planarity, and convex hull.
The complexity class $\operatorname{NTIME} [t( n )]$ is the set of decision problems that are accepted by a non-deterministic multi-tape Turing machine in $O ( t ( n ) )$ steps for inputs of length $n$. A non-deterministic Turning machine may make one of several possible moves at each step. One says that it "accepts an input" if at least one of its possible computations on that input is accepting. The time is the maximum number of steps that any computation may take on this input, not the exponentially greater number of steps required to simulate all possible computations on that input.
Non-deterministic polynomial time ($\operatorname{NP}$) is the set of decision problems accepted by a non-deterministic Turing machine in some polynomial time, $\operatorname { NP} = \operatorname { NTIME} [ n ^ { O ( 1 ) } ]$. For example, let $\operatorname{SAT}$ be the set of Boolean formulas that have some assignment of their Boolean variables making them true (cf. also Boolean algebra). The formula $\phi \equiv ( x _ { 1 } \vee x _ { 2 } ) \wedge ( \overline { x _ { 2 } } \vee \overline { x _ { 3 } } ) \wedge ( \overline { x _ { 1 } } \vee x _ { 3 } )$ is in $\operatorname{SAT}$ because the assignment that makes $x_{1} $ and $x _ { 3 }$ true and $x _ { 2 }$ false satisfies $\phi$. Given a formula with $k$ Boolean variables, a non-deterministic machine can non-deterministically write a binary string of length $k$ and then check if the assignment it has written down satisfies the formula, accepting if it does. Thus $\operatorname{SAT} \in \operatorname{NP}$. The decision versions of many important optimization problems, including travelling salesperson, graph colouring, clique, knapsack, bin packing and processor scheduling, are in $\operatorname{NP}$.
The complexity class $\operatorname{DSPACE}[s(n)]$ is the set of decision problems that are accepted by a deterministic Turing machine that uses at most $O ( t ( n ) )$ tape cells for inputs of length $n$. It is assumed that the input tape is read-only and space is only charged for the other tapes. Thus it makes sense to talk about space less than $n$.
Similarly one defines the non-deterministic space classes, $\operatorname{NSPACE}[s(n)]$. On inputs of length $n$, an $\operatorname{NSPACE}[s(n)]$ Turing machine uses at most $O ( s ( n ) )$ tape cells on each of its computations. One says it "accepts an input" if at least one of its computations on that input is accepting. The main space complexity classes are polynomial space, $\operatorname { PSPACE }= \operatorname { DSPACE } [ n ^ { O ( 1 ) } ]$; Logspace, $L = \operatorname{DSPACE} [\operatorname{log} n]$; and non-deterministic logspace, $\operatorname{NL} = \operatorname{NSPACE} [ \operatorname { log } n ]$.
For each of the above resources (deterministic and non-deterministic time and space) there is a hierarchy theorem saying that more of the given resource enables one to compute more decision problems. These theorems are proved by diagonalization arguments: use the greater amount of the resource to simulate all machines using the smaller amount, and do something different from the simulated machine in each case.
Hierarchy theorems.
See also [a11], [a10], [a4], [a20]. In the statement of these theorems the notion of a space- or time-constructible function is used. Recall that a function $s$ from the positive integers to itself is space constructible (respectively, time constructible) if and only if there is a deterministic Turing machine running in space $O ( s ( n ) )$ (respectively, time $O ( s ( n ) )$) that on every input of length $n$ computes the number $s ( n )$ in binary. Every reasonable function is constructible.
The following are hierarchy theorems:
1) For all space constructible $s ( n ) \geq \operatorname { log } n$, if
\begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { t ( n ) } { s ( n ) } = 0, \end{equation*}
then $\operatorname{DSPACE}[t(n)]$ is strictly contained in $\operatorname{DSPACE}[s(n)]$, and $\text{NSPACE} [t( n )]$ is strictly contained in $\operatorname{NSPACE}[s(n)]$.
2) For all time constructible $t ( n ) \geq n$, if
\begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } \frac { t ( n ) } { s ( n ) } = 0, \end{equation*}
then $\operatorname{NTIME} [t( n )]$ is strictly contained in $\text{NTIME} \, [ s ( n ) ]$.
3) For all time constructible $t ( n ) \geq n$, if
\begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } t ( n ) ( \operatorname { log } t ( n ) ) / s ( n ) = 0, \end{equation*}
then $\operatorname {DTIME}[t(n)]$ is strictly contained in $\operatorname{DTIME}[ s ( n ) ]$
The slightly stronger requirement in the last of the above theorems has to do with the extra factor of time $\operatorname{log} ( t ( n ) )$ that is required for a two-tape Turing machine to simulate a machine with more than two tapes. If one restricts attention to multi-tape Turing machines with a fixed number of tapes, then a strict hierarchy theorem for deterministic time results [a8].
Much less is know when comparing different resources: One can simulate $\operatorname{NTIME} [t( n )]$ in $\operatorname{DSPACE}[t(n)]$ by simulating all the non-deterministic computations in turn. One can simulate $\operatorname{DSPACE}[s(n)]$ in $\operatorname{DTIME}[ 2 ^ { O ( s ( n ) ) } ]$ because a $\operatorname{DSPACE}[s(n)]$ computation can be in one of at most $2 ^ { O ( s ( n ) ) }$ possible configurations.
Savitch's theorem provides a non-trivial relationship between deterministic and non-deterministic space [a19]: For $s ( n ) \geq \operatorname { log } n$,
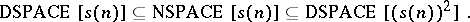 |
For each decision problem $S \subseteq \Sigma ^ {\color{blue} * }$, its complement $\bar{S} = \Sigma ^ {\color{blue} * } - S$ is also a decision problem. For each complexity class $\mathcal{C}$, define its complementary class by
\begin{equation*} \operatorname { co } \mathcal{C} = \{ S : \overline{S} \in \mathcal{C} \}. \end{equation*}
For deterministic classes $\mathcal{C}$, such as $P$, $L$ and 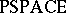 , it is obvious that ${\cal C} = \operatorname { co }\cal C$. However, this is much less clear for non-deterministic classes. Since the definitions of $\text{NTIME}$ and
, it is obvious that ${\cal C} = \operatorname { co }\cal C$. However, this is much less clear for non-deterministic classes. Since the definitions of $\text{NTIME}$ and 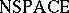 were made, it was widely believed that $\text{NP} \neq \operatorname{co} \text{NP}$ and $\text{NSPACE }[ n ] \neq\text{co NSPACE }[n]$. However, in 1987 the latter was shown to be false [a25], [a18]. In fact, the following Immerman–Szelepcsényi theorem holds: For $s ( n ) \geq \operatorname { log } n$, $\text{NSPACE} [ s ( n ) ] = \text { co } \text{NSPACE} [ s ( n ) ]$.
were made, it was widely believed that $\text{NP} \neq \operatorname{co} \text{NP}$ and $\text{NSPACE }[ n ] \neq\text{co NSPACE }[n]$. However, in 1987 the latter was shown to be false [a25], [a18]. In fact, the following Immerman–Szelepcsényi theorem holds: For $s ( n ) \geq \operatorname { log } n$, $\text{NSPACE} [ s ( n ) ] = \text { co } \text{NSPACE} [ s ( n ) ]$.
Even though complexity classes are all defined as sets of decision problems, one can define functions computable in a complexity class as follows. For a complexity class $\mathcal{C}$, define $F ( {\cal C} )$ to be the set of all polynomially-bounded functions $f : \Sigma ^ { \color{blue}* } \rightarrow \Sigma ^ { \color{blue} * }$ such that each bit of $f$ (thought of as a decision problem) is in $\mathcal{C}$ and $\text{co} \mathcal{C}$.
One compares the complexity of decision problems by reducing one to the other as follows. Let $A , B \subseteq \Sigma ^ { * }$. $A$ is reducible to $B$ ($A \leq B$) if and only if there exists a function $f \in F ( L )$ such that for all $w \in \Sigma ^ {\color{blue} * }$, $w \in A$ if and only if $f ( w ) \in B$. The question whether $w$ is a member of $A$ is thus reduced to the question of whether $f ( w )$ is a member of $B$. If $f ( w ) \in B$, then $w \in A$. Conversely, if $f ( w ) \notin B$, then $w \notin A$.
The complexity classes, i.e., $L$, $\operatorname{NL}$, $P$, $\operatorname{NP}$, 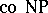 , and
, and 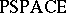 , are all closed under reductions in the following sense: If $\mathcal{C}$ is one of the above classes, $A \leq B$, and $B \in \mathcal{C}$, then $A \in \mathcal{C}$.
, are all closed under reductions in the following sense: If $\mathcal{C}$ is one of the above classes, $A \leq B$, and $B \in \mathcal{C}$, then $A \in \mathcal{C}$.
A problem $A$ is complete for complexity class $\mathcal{C}$ if and only if $A \in \mathcal{C}$ and for all $B \in \mathcal{C}$, $B < A$. If $\mathcal{C}$ is closed under reductions, then any complete problem, say $A$, characterizes the complexity class, because for all $B$, $B \in \mathcal{C}$ implies $B < A$.
Most natural complexity classes include a large number of interesting complete problems. See [a9], [a15], [a14] for substantial collections of problems that are complete for $\operatorname{NP}$, $P$, and $\operatorname{NL}$, respectively.
A non-deterministic machine can be thought of as a parallel machine with weak communication. At each step, each processor $p$ may create copies of itself and set them to work on slightly different problems. If any of these offspring ever reports acceptance to $p$, then $p$ in turn reports acceptance to its parent. Each processor thus reports the "or" of its children.
A. Chandra, D.C. Kozen and L. Stockmeyer generalized non-deterministic Turing machines to alternating Turing machines, in which there are "or" states, reporting the "or" of their children, and there are "and" states, reporting the "and" of their children. They proved the following alternation theorem [a3]: For $s ( n ) \geq \operatorname { log } n$ and $t ( n ) \geq n$,
\begin{equation*} \operatorname {ATIME}[ ( t ( n ) ) ^ { O ( 1 ) } ] = \operatorname { DSPACE } [ ( t ( n ) ) ^ { O ( 1 ) } ]; \end{equation*}
\begin{equation*} \operatorname { ASPACE } [ s ( n ) ] = \operatorname { DTIME } [ 2 ^ { O ( s ( n ) ) } ]. \end{equation*}
In particular, $\operatorname{ASPACE}[\operatorname{log} n] = P$ and $\operatorname{ATIME} [ n ^ { O ( 1 ) } ] = \operatorname { PSPACE }$.
Let the class $\text{ASPACETIME} \, [ s ( n ) , t ( n ) ]$ (respectively, $\text{ATIMEALT} [ t ( n ) , a ( n )]$) be the set of decision problems accepted by alternating machines simultaneously using space $s ( n )$ and time $t ( n )$ (respectively, time $t ( n )$ and making at most $a ( n )$ alternations between existential and universal states, and starting with existential). Thus $\operatorname{ATIMEALT}[ n ^ { O ( 1 ) } , 1 ] = \operatorname{NP}$. The polynomial-time hierarchy ($\operatorname{PH}$) is the set of decision problems accepted in polynomial time by alternating Turing machines making a bounded number of alternations between existential and universal states, $\operatorname{PH} = \operatorname{ATIMEALT} [ n ^ { O ( 1 ) } , O ( 1 ) ]$.
$\text{NC}$ is the set of decision problems recognizable by a parallel random access machine (a PRAM) using polynomially much hardware and parallel time $( \operatorname { log } n ) ^ { O ( 1 ) }$. $\text{NC}$ is often studied using uniform classes of acyclic circuits of polynomial size and depth $( \operatorname { log } n ) ^ { O ( 1 ) }$. $\text{NC}$ is characterized via alternating complexity in the following way,
\begin{equation*} \operatorname{NC} = \text { ASPACETIME } [ \operatorname { log } n , ( \operatorname { log } n ) ^ { O ( 1 ) } ]. \end{equation*}
A decision problem is complex if and only if it has a complex description. This leads to a characterization of complexity via logic. The input object, e.g., a string or a graph, is thought of as a (finite) logical structure. R. Fagin characterized $\operatorname{NP}$ as the set of second-order expressible properties ($\operatorname{NP} = \operatorname{SO} ( \exists )$), N. Immerman and M.Y. Vardi characterized $P$ as the set of properties expressible in first-order logic plus a least-fixed-point operator ($P = \operatorname{FO} ( \operatorname{LFP} )$). In fact, all natural complexity classes have natural descriptive characterizations [a7], [a24], [a22], [a5], [a23].
A probabilistic Turing machine is one that may flip a series of fair coins as part of its computation. A decision problem $S$ is in bounded probabilistic polynomial time ($\operatorname {BPP}$) if and only if there is a probabilistic polynomial-time Turing machine $M$ such that for all inputs $w$, if $( w \in S )$, then $\mathsf{P}(M \ \text{accepts} \ w) \geq 2 / 3$, and if $( w \notin S )$, then $P(M\, \text{accepts}\, w)\leq 1 / 3$.
It follows by running $M ( w )$ polynomially many times that the probability of error can be made at most $2 ^ { - n ^ { k } }$ for any fixed $k$ and inputs of length $n$. It is believed that $P = \operatorname {BPP}$. An important problem in $\operatorname {BPP}$ that is not known to be in $P$ is primality, [a21].
Recent work (1998) on randomness and cryptography has led to a new and surprising characterization of $\operatorname{NP}$ via interactive proofs [a1]. This in turn has led to tight bounds on how closely many $\operatorname{NP}$ optimization problems can be approximated in polynomial time, assuming that $P \neq \text{NP}$ [a13].
It is known that 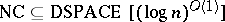 , so by the space hierarchy theorem $\text{NC}$ (and thus of course $\operatorname{NL}$ and $L$) is strictly contained in
, so by the space hierarchy theorem $\text{NC}$ (and thus of course $\operatorname{NL}$ and $L$) is strictly contained in  . Strong lower bounds have been proved on some circuit complexity classes below $L$ [a2], [a6], [a12], [a17]; but even now (2001), thirty years after the introduction of the classes $P$ and $\operatorname{NP}$, no other inequality concerning the following containments, including that $L$ is not equal to $\operatorname{PH}$, is known:
. Strong lower bounds have been proved on some circuit complexity classes below $L$ [a2], [a6], [a12], [a17]; but even now (2001), thirty years after the introduction of the classes $P$ and $\operatorname{NP}$, no other inequality concerning the following containments, including that $L$ is not equal to $\operatorname{PH}$, is known:
\begin{equation*} L \subseteq \operatorname{NL} \subseteq \operatorname{NC} \subseteq P \subseteq \operatorname{NP} \subseteq \operatorname{PH} \subseteq \operatorname{PSPACE}. \end{equation*}
For further reading, an excellent textbook on computational complexity is [a16].
References
| [a1] | S. Arora, C. Lund, R. Motwani, M. Sudan, M. Szegedy, "Proof verification and the hardness of approximation problems" J. Assoc. Comput. Mach. , 45 : 3 (1998) pp. 501–555 |
| [a2] | M. Ajtai, "$\Sigma ^ { 1 _ { 1 }}$ formulae on finite structures" Ann. Pure Appl. Logic , 24 (1983) pp. 1–48 |
| [a3] | A. Chandra, L. Stockmeyer, "Alternation" , Proc. 17th IEEE Symp. Found. Computer Sci. (1976) pp. 151–158 |
| [a4] | S.A. Cook, "A hierarchy for nondeterministic time complexity" J. Comput. Syst. Sci. , 7 : 4 (1973) pp. 343–353 |
| [a5] | H.-D. Ebbinghaus, J. Flum, "Finite model theory" , Springer (1995) |
| [a6] | M. Furst, J.B. Saxe, M. Sipser, "Parity, circuits, and the polynomial-time hierarchy" Math. Systems Th. , 17 (1984) pp. 13–27 |
| [a7] | R. Fagin, "Generalized first-order spectra and polynomial-time recognizable sets" R. Karp (ed.) , Complexity of Computation (SIAM-AMS Proc.) , 7 , Amer. Math. Soc. (1974) pp. 27–41 |
| [a8] | M. Fürer, "The tight deterministic time hierarchy" , 14th ACM STOC Symp. (1982) pp. 8–16 |
| [a9] | M.R. Garey, D.S. Johnson, "Computers and intractability" , Freeman (1979) |
| [a10] | J. Hartmanis, P.M. Lewis, R.E. Stearns, "Hierarchies of memory limited computations" , Sixth Ann. IEEE Symp. Switching Circuit Theory and Logical Design (1965) pp. 179–190 |
| [a11] | J. Hartmanis, R. Stearns, "On the computational complexity of algorithms" Trans. Amer. Math. Soc. , 117 : 5 (1965) pp. 285–306 |
| [a12] | J. Hastad, "Almost optimal lower bounds for small depth circuits" , 18th ACM STOC Symp. (1986) pp. 6–20 |
| [a13] | "Approximation algorithms for NP hard problems" D. Hochbaum (ed.) , PWS (1997) |
| [a14] | N. Jones, E. Lien, W. Laaser, "New problems complete for nondeterministic logspace" Math. Systems Th. , 10 (1976) pp. 1–17 |
| [a15] | R. Greenlaw, H.J. Hoover, L. Ruzzo, "Limits to parallel computation: P-completeness theory" , Oxford Univ. Press (1995) |
| [a16] | C.H. Papadimitriou, "Complexity" , Addison-Wesley (1994) |
| [a17] | A.A. Razborov, "Lower bounds on the size of bounded depth networks over a complete basis with logical addition" Math. Notes , 41 (1987) pp. 333–338 Mat. Zametki , 41 (1987) pp. 598–607 |
| [a18] | R. Szelepcsényi, "The method of forced enumeration for nondeterministic automata" Acta Inform. , 26 (1988) pp. 279–284 |
| [a19] | W. Savitch, "Relationships between nondeterministic and deterministic tape complexities" J. Comput. Syst. Sci. , 4 (1970) pp. 177–192 |
| [a20] | J.I. Seiferas, M.J. Fischer, A.R. Meyer, "Refinements of nondeterministic time an space hierarchies" , Proc. Fourteenth Ann. IEEE Symp. Switching and Automata Theory (1973) pp. 130–137 |
| [a21] | R. Solovay, V. Strassen, "A fast Monte-Carlo test for primality" SIAM J. Comput. , 6 (1977) pp. 84–86 |
| [a22] | M.Y. Vardi, "Complexity of relational query languages" , 14th Symp. Theory of Computation (1982) pp. 137–146 |
| [a23] | N. Immerman, "Descriptive complexity" , Graduate Texts in Computer Sci. , Springer (1999) |
| [a24] | N. Immerman, "Relational queries computable in polynomial time" , 14th ACM STOC Symp. (1982) pp. 147–152 (Revised version: Inform. & Control 68 (1986), 86-104) |
| [a25] | N. Immerman, "Nondeterministic space is closed under complementation" SIAM J. Comput. , 17 : 5 (1988) pp. 935–938 |
Computational complexity classes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Computational_complexity_classes&oldid=16056