Complex structure

A complex structure on a real vector space is the structure of a complex vector space on that is compatible with the original real structure. The complex structure on is completely determined by the operator of multiplication by the number , the role of which can be taken by an arbitrary linear transformation satisfying , where is the identity. Therefore, a transformation of this type is often called a complex structure on . If is endowed with a complex structure and is a basis of this space over , then forms a basis of it over 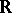, so that 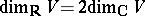. If is a complex structure on 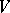then the complexification 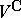of decomposes into a direct sum , where 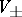are the eigen spaces of the transformation 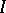extended to corresponding to the eigen values 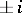, and . Conversely, each complex subspace 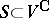such that determines a complex structure on for which .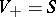

Any two complex structures on a 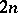-dimensional real space 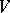can be mapped into each other by some automorphism of . The set of all complex structures on is thus a homogeneous space of the group and is identified with the quotient space , where is the subgroup of non-singular matrices of the form

A complex structure on a differentiable manifold is the structure of a complex-analytic manifold (cf. Analytic manifold). If 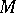is a differentiable manifold, then a complex structure on is a complex-analytic atlas on 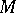that is compatible with the real differentiable atlas defined on . Here . A complex structure on 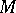induces a complex structure on each tangent space 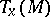, and therefore induces on an almost-complex structure which completely determines it.

References

[1]	A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French)
[2]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)