Completely-reducible set

A set 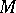of linear operators on a topological vector space 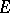with the following property: Any closed subspace in 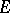that is invariant with respect to 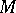has a complement in 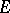that is also invariant with respect to 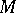. In a Hilbert space 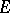any set 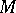that is symmetric with respect to Hermitian conjugation is completely reducible. In particular, any group of unitary operators is a completely-reducible set. A representation 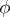of an algebra (group, ring, etc.) is called completely reducible if the set is completely reducible. If is a compact group or a semi-simple connected Lie group (Lie algebra), any representation of 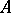in a finite-dimensional vector space is completely reducible (the principle of complete reducibility).

References

[1]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)

Comments

The principle of complete reducibility is commonly referred to as Weyl's theorem (cf. [a1], Chapt. 2 Sect. 6).

References

[a1]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972)