Completely-reducible matrix group
A matrix group 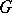 over an arbitrary fixed field
over an arbitrary fixed field 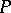 , all elements of which may be reduced by simultaneous conjugation by some matrix over
, all elements of which may be reduced by simultaneous conjugation by some matrix over 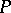 to block-diagonal form, i.e. to the form
to block-diagonal form, i.e. to the form
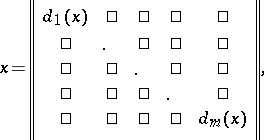 |
where  ,
, 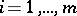 , are square matrices, the remaining places being filled by zeros, and each matrix group
, are square matrices, the remaining places being filled by zeros, and each matrix group 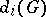 is irreducible (cf. Irreducible matrix group). In the language of transformations, a group
is irreducible (cf. Irreducible matrix group). In the language of transformations, a group 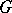 of linear transformations of a finite-dimensional vector space
of linear transformations of a finite-dimensional vector space 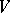 over a field is said to be completely reducible if any one of the following equivalent conditions is met: 1) Any subspace of
over a field is said to be completely reducible if any one of the following equivalent conditions is met: 1) Any subspace of  which is
which is 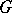 -invariant has a
-invariant has a  -invariant direct complement (cf. Invariant subspace); 2)
-invariant direct complement (cf. Invariant subspace); 2) 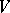 is decomposable into the direct sum of minimal
is decomposable into the direct sum of minimal 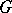 -invariant subspaces; or 3)
-invariant subspaces; or 3) 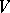 is generated by the minimal
is generated by the minimal  -invariant subspaces. Every finite matrix group
-invariant subspaces. Every finite matrix group 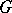 over a field whose characteristic does not divide the order of
over a field whose characteristic does not divide the order of 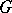 is completely reducible. Every normal subgroup of a completely-reducible matrix group is itself completely reducible.
is completely reducible. Every normal subgroup of a completely-reducible matrix group is itself completely reducible.
References
| [1] | Yu.I. Merzlyakov, "Rational groups" , Moscow (1987) (In Russian) |
| [2] | M. Hall, "Group theory" , Macmillan (1959) |
Comments
References
| [a1] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
Completely-reducible matrix group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completely-reducible_matrix_group&oldid=13792