Difference between revisions of "Completely-integrable differential equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Frobenius, "Ueber das Pfaffsche Problem" ''J. Reine Angew. Math.'' , '''82''' (1877) pp. 230–315</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, "On the orbit theory of general dynamic systems" ''Mat. Sb.'' , '''23 (65)''' : 2 (1948) pp. 161–186 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.P. Novikov, "Topology of foliations" ''Trans. Moscow Math. Soc.'' , '''14''' (1965) pp. 268–304 ''Trudy Moskov. Mat. Obshch.'' , '''14''' (1965) pp. 248–278 {{MR|0200938}} {{ZBL|0247.57006}} </TD></TR></table> |
| Line 36: | Line 36: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1945)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1–2''' , Interscience (1963–1969) {{MR|1393941}} {{MR|1393940}} {{MR|0238225}} {{MR|1533559}} {{MR|0152974}} {{ZBL|0526.53001}} {{ZBL|0508.53002}} {{ZBL|0175.48504}} {{ZBL|0119.37502}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
An equation of the form
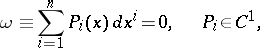 | (*) |
for which an  -dimensional integral manifold passes through each point of a certain domain in the space
-dimensional integral manifold passes through each point of a certain domain in the space  . A necessary and sufficient condition for complete integrability of the differential equation (*) is the Frobenius condition
. A necessary and sufficient condition for complete integrability of the differential equation (*) is the Frobenius condition  , where
, where  is the symbol of the exterior product [1]. If
is the symbol of the exterior product [1]. If  , this condition has the form:
, this condition has the form:
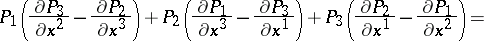 |
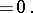 |
Instead of equation (*) the following system of equations is sometimes considered [2]:
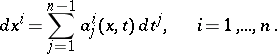 |
In this case the conditions of complete integrability assume the form:
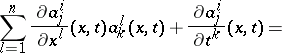 |
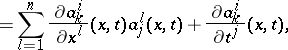 |
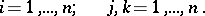 |
The family of integral manifolds of a completely-integrable differential equation is a foliation [3].
References
| [1] | G. Frobenius, "Ueber das Pfaffsche Problem" J. Reine Angew. Math. , 82 (1877) pp. 230–315 |
| [2] | V.V. Nemytskii, "On the orbit theory of general dynamic systems" Mat. Sb. , 23 (65) : 2 (1948) pp. 161–186 (In Russian) |
| [3] | S.P. Novikov, "Topology of foliations" Trans. Moscow Math. Soc. , 14 (1965) pp. 268–304 Trudy Moskov. Mat. Obshch. , 14 (1965) pp. 248–278 MR0200938 Zbl 0247.57006 |
Comments
The exterior product 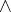 is also called the outer product.
is also called the outer product.
An 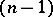 -dimensional submanifold
-dimensional submanifold 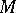 of
of 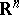 is an integral manifold of (*) if the restriction of
is an integral manifold of (*) if the restriction of 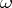 to
to  is zero; cf. also Pfaffian equation. Another (dual) way to formulate this is as follows. Let
is zero; cf. also Pfaffian equation. Another (dual) way to formulate this is as follows. Let 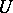 be an open subset where
be an open subset where 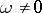 . For each
. For each  let
let 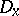 be the set of all (tangent) vectors
be the set of all (tangent) vectors 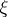 at
at  such that
such that 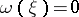 . Then
. Then 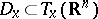 is an
is an 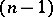 -dimensional subspace and the
-dimensional subspace and the  define a distribution on
define a distribution on 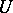 . An integral manifold
. An integral manifold 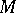 of
of  (or of the equation
(or of the equation  ) is now an
) is now an  -dimensional submanifold of
-dimensional submanifold of 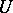 such that
such that 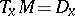 for all
for all  . A distribution
. A distribution 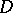 on
on 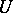 is called involutive if for all vector fields
is called involutive if for all vector fields  on
on 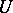 such that
such that 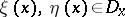 for all
for all  also
also  for all
for all  . The Frobenius integrability condition
. The Frobenius integrability condition  is equivalent in these terms to the condition that the distribution defined by
is equivalent in these terms to the condition that the distribution defined by 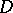 be involutive. All this generalizes to systems of equations
be involutive. All this generalizes to systems of equations 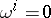 ,
, 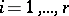 ; cf. Integrable system.
; cf. Integrable system.
The phase completely-integrable system (completely-integrable Hamiltonian system), completely-integrable Hamiltonian equation on an  -dimensional manifold refers to a rather different property, viz. that of having
-dimensional manifold refers to a rather different property, viz. that of having  (including the Hamiltonian (function) itself) integrals in involution; cf. Hamiltonian system.
(including the Hamiltonian (function) itself) integrals in involution; cf. Hamiltonian system.
References
| [a1] | E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1945) |
| [a2] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) MR1393941 MR1393940 MR0238225 MR1533559 MR0152974 Zbl 0526.53001 Zbl 0508.53002 Zbl 0175.48504 Zbl 0119.37502 |
Completely-integrable differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completely-integrable_differential_equation&oldid=13469