Complete system
closed system (of differential equations)
A system of first-order partial differential equations:
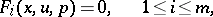 | (1) |
 |
 |
with the following property: For any set of numbers 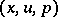 satisfying (1), the equation
satisfying (1), the equation
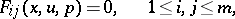 |
is valid, where 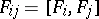 are the Jacobi brackets.
are the Jacobi brackets.
The completeness condition may be formulated somewhat differently for a linear homogeneous system. The Jacobi brackets in that case are linear in the variables 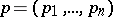 ; if the system is written in the form
; if the system is written in the form
 |
where the 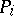 are linear first-order differential operators, then these brackets correspond to the commutators
are linear first-order differential operators, then these brackets correspond to the commutators 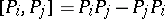 . The system is complete if all commutators
. The system is complete if all commutators 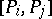 can be expressed as linear combinations of the
can be expressed as linear combinations of the 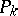 's with coefficients depending only on
's with coefficients depending only on 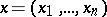 .
.
If  is the joint solution of the two equations
is the joint solution of the two equations
 |
then  is also a solution of the equation
is also a solution of the equation
 | (2) |
An arbitrary system of the form (1) is usually extended to a complete one by adding new independent equations to it that have been obtained from the old ones by means of the formation of Jacobi brackets. In this extension, in accordance with (2), none of the solutions will be lost if the system is generally solvable.
A property of the system is that it is completely invariant under those non-singular transformations of the variables 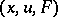 for which the meaning of the differential equations is retained. These transformations include, for example, diffeomorphisms
for which the meaning of the differential equations is retained. These transformations include, for example, diffeomorphisms 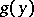 ,
, 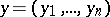 , and also transformations of the following type. Let
, and also transformations of the following type. Let 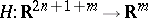 be a smooth mapping such that
be a smooth mapping such that
 |
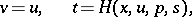 |
 |
is a diffeomorphism 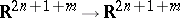 . This transforms the system (1) into a system
. This transforms the system (1) into a system
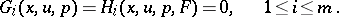 |
References
| [1] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 2. Partielle Differentialgleichungen erster Ordnung für die gesuchte Funktion , Akad. Verlagsgesell. (1944) |
| [2] | N.M. Gyunter, "Integrating first-order partial differential equations" , Leningrad-Moscow (1934) (In Russian) |
| [3] | C. Carathéodory, "Calculus of variations and partial differential equations of the first order" , 1 , Holden-Day (1965) (Translated from German) |
| [4] | E. Goursat, "Leçons sur l'intégration des équations aux dérivées partielles du premier ordre" , Hermann (1891) |
Comments
A system (1) can be rewritten in the form:
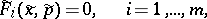 | (a1) |
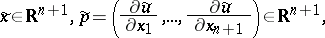 |
where 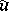 defines
defines  implicitly:
implicitly:
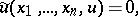 |
and 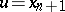 . (The system (1) may admit of singular solutions not represented by (a1), see [1].) The Jacobi brackets
. (The system (1) may admit of singular solutions not represented by (a1), see [1].) The Jacobi brackets 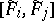 thus reduce to the Poisson brackets
thus reduce to the Poisson brackets 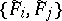 .
.
The system (a1) defines level sets of the functions 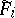 ,
, 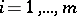 , on the cotangent bundle
, on the cotangent bundle 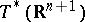 . (a1) is complete if the Poisson brackets
. (a1) is complete if the Poisson brackets 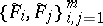 vanish on the intersection
vanish on the intersection 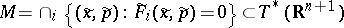 . (a1) is in involution in a neighbourhood
. (a1) is in involution in a neighbourhood 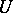 of
of 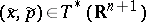 if the Poisson brackets vanish identically on
if the Poisson brackets vanish identically on 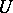 and, moreover,
and, moreover, 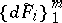 are linearly independent on
are linearly independent on 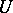 .
.
(a1) is in involution in a neighbourhood of 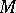 if it is complete and the linear independency condition holds on
if it is complete and the linear independency condition holds on 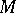 . Being in involution is a necessary condition for the existence of a solution of the system (1) (or (a1)), cf. Darboux theorem and [a1], Sect. 21.1. As suggested in the main article, these considerations generalize to systems defined on general differentiable manifolds.
. Being in involution is a necessary condition for the existence of a solution of the system (1) (or (a1)), cf. Darboux theorem and [a1], Sect. 21.1. As suggested in the main article, these considerations generalize to systems defined on general differentiable manifolds.
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) |
Complete system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_system&oldid=18756