Complete set
in a topological vector space  over a field
over a field 
A set  such that the set of linear combinations of the elements from
such that the set of linear combinations of the elements from  is (everywhere) dense in
is (everywhere) dense in  , i.e. the closed subspace generated by the set
, i.e. the closed subspace generated by the set  , i.e. the closed linear hull of
, i.e. the closed linear hull of  , coincides with
, coincides with  . For example, in the normed space
. For example, in the normed space  of continuous functions on
of continuous functions on 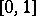 with values in
with values in 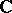 the set
the set 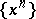 is a complete set. If
is a complete set. If 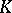 is a non-discretely normed field, each absorbing set (and in particular each neighbourhood of zero in
is a non-discretely normed field, each absorbing set (and in particular each neighbourhood of zero in  ) is a complete set.
) is a complete set.
In order for  ,
, 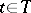 , to be a complete set in the weak topology
, to be a complete set in the weak topology 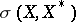 of a space
of a space 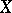 it is necessary and sufficient that there exist an index
it is necessary and sufficient that there exist an index 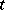 such that
such that  for each
for each 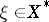 ; this means that no closed hyperplane contains all the elements
; this means that no closed hyperplane contains all the elements  , i.e. that
, i.e. that  is a total set. Moreover, if
is a total set. Moreover, if 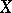 is a locally convex space, a complete set in the weak topology will be a complete set in the initial topology also.
is a locally convex space, a complete set in the weak topology will be a complete set in the initial topology also.
Comments
Of course, a complete set in a topological vector space can also mean a set 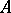 such that every Cauchy sequence in
such that every Cauchy sequence in 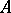 converges in
converges in 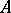 ; and this is by far the most frequently occurring meaning of the phrase. For the notion of an absorbing set cf. Topological vector space.
; and this is by far the most frequently occurring meaning of the phrase. For the notion of an absorbing set cf. Topological vector space.
Complete set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_set&oldid=18761